ЬтФПФкШн
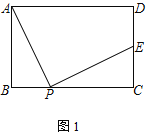
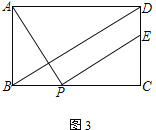
ЁОЬтФПЁПвбжЊОиаЮABCDЃЌЕуPЮЊБпBCЩЯвЛЖЏЕуЃЌСЌНгAPЃЌНЋЯпЖЮAPШЦЕуPЫГЪБеыа§зЊ90ЁуЃЌЕуAЧЁКУТфдкжБЯпCDЩЯЕуEДІ
(1) ШчЭМ1ЃЌЕуEдкЯпЖЮCDЩЯЃЌЧѓжЄЃКADЃЋDEЃН2AB
(2) ШчЭМ2ЃЌЕуEдкЯпЖЮCDЕФбгГЄЯпЩЯЃЌЧвЕуD ЮЊЯпЖЮCEЕФжаЕуЃЌдкЯпЖЮBDЩЯШЁЕуFЃЌСЌНгAFЁЂPFЃЌШєAF=ABЃЌЧѓжЄЃКЁЯAPFЃНЁЯADB
(3) ШчЭМ3ЃЌЕуEдкЯпЖЮCDЩЯЃЌСЌНгBDЃЎШєABЃН2ЃЌBDЁЮPEЃЌдђDEЃН___________ ЃЈжБНгаДГіНсЙћЃЉ
ЁОД№АИЁПЃЈ1ЃЉЯъМћНтЮіЃЛЃЈ2ЃЉЯъМћНтЮіЃЛЃЈ3ЃЉ![]()
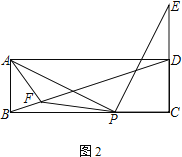
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉгУЭЌНЧЕФгрНЧЯрЕШЕУГіЁЯBAP=ЁЯCPEЃЌНјЖјХаЖЯГіЁїABPЁеЁїPCEЃЌМДПЩЕФЕУГіAB=PC=CDЃЌBP=CEЃЌзюКѓгУЯрЕШЕФЯпЖЮДњЛЛМДПЩЃЛ
ЃЈ2ЃЉЯШХаЖЯГіЫФБпаЮABDEЪЧЦНааЫФБпаЮдђгаBDЁЮAEЃЌМДПЩЕУЕНЃЌ ![]() дйХаЖЯГіЃЌЁїAPFЁеЁїEPDЃЌдђгаЁЯAFP=ЁЯDEPЃЌзюКѓгУШ§НЧаЮЕФЭтНЧКЭЕШНЧДњЛЛМДПЩЃЛ
дйХаЖЯГіЃЌЁїAPFЁеЁїEPDЃЌдђгаЁЯAFP=ЁЯDEPЃЌзюКѓгУШ§НЧаЮЕФЭтНЧКЭЕШНЧДњЛЛМДПЩЃЛ
ЃЈ3ЃЉЯШНшжњЃЈ1ЃЉЕФНсТлЕУГіPC=AB=2, AD=4DEЃЌдйХаЖЯГіЁїCPEЁзЁїCBDЃЌдђга![]() зюКѓДњжЕНтЙигк
зюКѓДњжЕНтЙигк![]() ЕФЗНГЬМДПЩЃЎ
ЕФЗНГЬМДПЩЃЎ
ЪдЬтНтЮіЃК(1)ЁпЫФБпаЮABCDЪЧОиаЮЃЌ
Ёр![]()
Ёр![]()
Ёп![]()
Ёр![]()
ЁрЁЯBAP=ЁЯCPEЃЌ
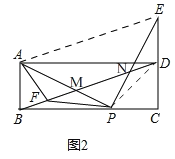
дкЁїABPКЭЁїPCEжа, 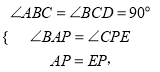
ЁрЁїABPЁеЁїPCEЃЌ
ЁрAB=PC=CDЃЌBP=CEЃЌ
ЁрAD+DE=BC+DE=BP+PC+DE=CE+CP+DE=CP+CD=2ABЃЛ
(2)ШчЭМ,
ЁпAB=AFЃЌ
ЁрЁЯABF=ЁЯAFBЃЌ
ЁпABЁЮDCЃЌ
ЁрЁЯABF=ЁЯBDCЃЌ
ЁрЁЯAFB=ЁЯBDCЃЌ
ЁрЁЯAFD=ЁЯEDFЃЌ
ЁпAB=CD=DE,ABЁЮCDЃЌ
ЁрЫФБпаЮABDEЪЧЦНааЫФБпаЮЃЌ
ЁрBDЁЮAEЃЌ
Ёп![]()
Ёр![]()
Ёр![]()
ЁпBDЁЮAEЃЌ
Ёр![]()
ЁпЁЯAFD=ЁЯEDFЃЌ
ЁрЁЯFAE=ЁЯDEAЃЌ
ЁпЁЯPAE=ЁЯPEAЃЌ
ЁрЁЯFAP=ЁЯDEPЃЌ
дкЁїAPFКЭЁїEPDжа, 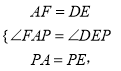
ЁрЁїAPFЁеЁїEPDЃЌ
ЁрЁЯAFP=ЁЯDEPЃЌ
ЁпЁЯAFD=ЁЯEDFЃЌ
ЁрЁЯPFD=ЁЯPDFЃЌ
дкRtЁїPCDжаЃЌPC=PDЃЌ
Ёр![]() Ёр
Ёр![]()
Ёр![]()
Ёп![]()
Ёр![]()
ЁрЁЯAPF=ЁЯADBЃЛ
(3)гЩ(1)жЊ,ЁїABPЁеЁїPCEЃЌ
ЁрPC=AB=2,гЩ(1)жЊЃЌAD+DE=2AB=4ЃЌ
ЁрAD=4DEЃЌ
ЁпDBЁЮPEЃЌ
ЁрЁїCPEЁзЁїCBDЃЌ
Ёр![]()
ЁпCB=AD=4DEЃЌCD=AB=2ЃЌCE=CDDE=2DEЃЌ
Ёр![]()
Ёр![]() (гЩгкЕуEдкЯпЖЮCDЩЯ,ЧвCD=2,ЫљвдЩсШЅ)Лђ
(гЩгкЕуEдкЯпЖЮCDЩЯ,ЧвCD=2,ЫљвдЩсШЅ)Лђ![]()
МДЃК ![]()
ЙЪД№АИЮЊЃК ![]()

ЁОЬтФПЁПЯТБэЪЧЖўДЮКЏЪ§y=ax2+bx+cЕФВПЗжx,yЕФЖдгІжЕЃК
x | Ё | Ѓ1 | Ѓ | 0 |
| 1 |
| 2 |
| 3 | Ё |
y | Ё | 2 |
| Ѓ1 | Ѓ | Ѓ2 | Ѓ | Ѓ1 |
| 2 | Ё |
ЃЈ1ЃЉДЫЖўДЮКЏЪ§ЭМЯѓЕФЖЅЕузјБъЪЧ ЃЛ
ЃЈ2ЃЉЕБХзЮяЯпy=ax2+bx+cЕФЖЅЕудкжБЯпy=x+nЕФЯТЗНЪБЃЌnЕФШЁжЕЗЖЮЇЪЧ ЁЃ