题目内容
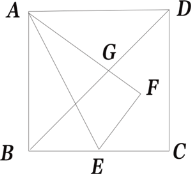
【题目】如图，已知正方形ABCD的边长为6，E为BC的中点，将△ABE沿直线AE折叠后，点B落在点F处，AF交对角线BD于点G，则FG的长是___________.
【答案】
【解析】
建立以B为原点的平面直角坐标系，运用勾股定理求出FM的长度，求出F点坐标，可求得 
及
，联立可求得
，利用长度公式即可求出FG的长度.
解：建立如图平面直角坐标系
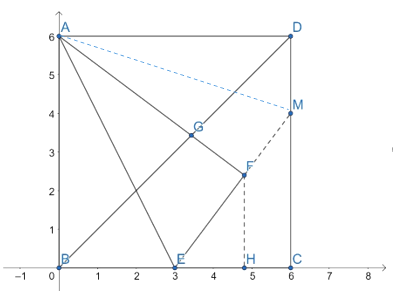
设延长EF交CD于M，连AM,过F作FH⊥BC于H
在正方形ABCD中∠ABC=∠ADC=90°，AB=AD
折叠可知△ABE≌△AFE
∴∠AFE=∠ABE=90°，AB=AF
∴∠AFM=∠ADM=90°，AF=AD
又∵AM=AM
∴△AFM≌△ADM
∴设FM=DM=x，MC=6-x
在Rt△ECM中，
∴
∴x=2
∵FH∥CM
∴
∴
∴
∴
∴
∴
∵B（0，0），D（6，6）
∴
∴
∴
∴
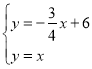
故答案为：
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
