Question

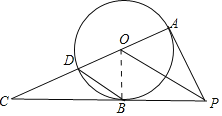
【题目】如图，PA是⊙O的切线，A为切点．B为⊙O上一点，连接AO并延长，交⊙O于点D．交PB的延长线于点C连接PO，若PA＝PB．

（1）求证：PB是⊙O的切线；

（2）连接DB，若∠C＝30°，求证：D是CO的中点．

Answer 1

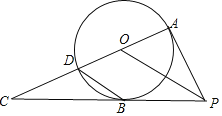
【答案】（1）证明见解析；（2）证明见解析.

【解析】

（1）连接OB，利用SSS证明△OAP与△OBP全等，进而利用切线的判定证明即可；

（2）利用含30°的直角三角形的性质证明即可．

证明：（1）连接OB，

在△OAP与△OBP中

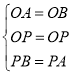
∴△OAP≌△OBP（SSS），

∴∠OAP＝∠OBP＝90°，

∴PB是⊙O的切线；

（2）∵∠OBP＝90°，

∵∠C＝30°，

∴OC＝2OB，

∵OB＝OD，

∴OD＝DC，

即D是CO的中点．