Question

【题目】如图，B，D分别在CF和EF上，CB＝ED，CA＝EA，∠C＝∠E，连接AB，AD．

（1）求证：AB＝AD；

（2）求证：BF＝DF．

Answer 1

【答案】（1）证明见解析；（2）证明见解析.

【解析】

（1）由“SAS”可证△ABC≌△ADE，可得AB=AD；
（2）由全等三角形的性质和等腰三角形的性质可得∠DBF=∠BDF，可得BF=DF．

证明：（1）∵CB＝ED，∠C＝∠E，CA＝EA，

∴△ABC≌△ADE（SAS）

∴AB＝AD；

（2）如图，连接BD，

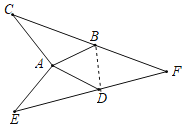
∵△ABC≌△ADE，

∴∠ABC＝∠ADE，

∴∠ABF＝∠ADF，

∵AB＝AD，

∴∠ABD＝∠ADB，

∴∠ABF﹣∠ABD＝∠ADF﹣∠ADB，

∴∠DBF＝∠BDF，

∴BF＝DF．