题目内容
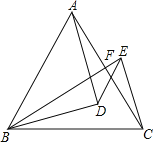
【题目】如图,△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,F为EC的中点,连接AF.写出AF与BD的数量关系和位置关系,并说明理由.

【答案】AF=![]() BD,AF⊥BD,理由见解析.
BD,AF⊥BD,理由见解析.
【解析】
过点C作CG∥AE交直线AF于G,直线AF交BD于H,证明△CGF≌△EAF(AAS),得出CG=AE,AF=GF,得出AF=![]() AG,证明△BAD≌△ACG(SAS),得出BD=AG,∠ABD=∠CAG,进而得出结论.
AG,证明△BAD≌△ACG(SAS),得出BD=AG,∠ABD=∠CAG,进而得出结论.
AF=![]() BD,AF⊥BD,理由如下:
BD,AF⊥BD,理由如下:
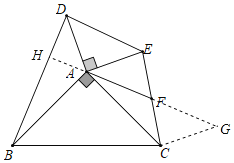
过点C作CG∥AE交直线AF于G,直线AF交BD于H,如图所示:
则∠G=∠EAF,∠EAC+∠ACG=180°,
∵F为EC的中点,
∴CF=EF,
在△CGF和△EAF中,
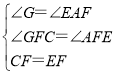 ,
,
∴△CGF≌△EAF(AAS),
∴CG=AE,AF=GF,
∴AF=![]() AG,
AG,
∵△ABC和△ADE均为等腰直角三角形,∠BAC=∠DAE=90°,
∴AB=AC,AD=AE,∠EAC+∠BAD=360°-90°-90°=180°,∠CAG+∠BAH=90°,
∴AD=CG,∠BAD=∠ACG,
在△BAD和△ACG中,
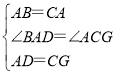 ,
,
∴△BAD≌△ACG(SAS),
∴BD=AG,∠ABD=∠CAG,
∴AF=![]() BD,∠ABD+∠BAH=90°,
BD,∠ABD+∠BAH=90°,
∴AF⊥BD.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目