题目内容
【题目】如图，在Rt△ABC中，∠BAC=90°，AB=3，M为边BC上的点，连接AM．如果将△ABM沿直线AM翻折后，点B恰好落在边AC的中点处，那么点M到AC的距离是_____．
【答案】2
【解析】
如图，作ME⊥AC于E，MF⊥AB于F，点D为AC的中点，根据折叠的性质得AD=AB=3，∠BAM=∠CAM，则AC=2AD=6，根据角平分线定理得ME=MF，然后利用面积法得到
MFAB+MEAC=ABAC，即3ME+6ME=3×6，解得ME=2．
如图,
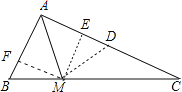
作ME⊥AC于E，MF⊥AB于F，点D为AC的中点，
∵△ABM沿直线AM翻折后，点B恰好落在边AC的中点D处，
∴AD=AB=3,∠BAM=∠CAM=45
，
∴AC=2AD=6，ME=MF，
∵S△ABM+S△AMC=S△ABC，
∴MF
AB+MEAC=ABAC，
∴3ME+6ME=3×6，
∴ME=2，
即点M到AC的距离是2.
故答案为2.
练习册系列答案
相关题目
【题目】抛物线
上部分点的横坐标
，纵坐标
的对应值如下表：
| … |
|
|
|
|
| … |
| … |
|
|
|
|
| … |
小聪观察上表，得出下面结论：①抛物线与轴的一个交点为
；②函数的最大值为
；③抛物线的对称轴是
；④在对称轴左侧，随增大而增大．其中正确有（ ）
A. 0个 B. 1个 C. 2个 D. 3个