题目内容
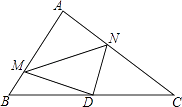
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K-∠H=33°,则∠K=__________.

【答案】82°
【解析】
分别过K、H作AB的平行线MN和RS,根据平行线的性质和角平分线的性质可用∠ABK和∠DCK分别表示出∠H和∠K,从而可找到∠H和∠K的关系,结合条件可求得∠K.
如图,分别过K、H作AB的平行线MN和RS.
∵AB∥CD,∴AB∥CD∥RS∥MN,∴∠RHB=∠ABE![]() ∠ABK,∠SHC=∠DCF
∠ABK,∠SHC=∠DCF![]() ∠DCK,∠NKB+∠ABK=∠MKC+∠DCK=180°,∴∠BHC=180°﹣∠RHB﹣∠SHC=180°
∠DCK,∠NKB+∠ABK=∠MKC+∠DCK=180°,∴∠BHC=180°﹣∠RHB﹣∠SHC=180°![]() (∠ABK+∠DCK),∠BKC=180°﹣∠NKB﹣∠MKC=180°﹣(180°﹣∠ABK)﹣(180°﹣∠DCK)=∠ABK+∠DCK﹣180°,∴∠BKC=360°﹣2∠BHC﹣180°=180°﹣2∠BHC.
(∠ABK+∠DCK),∠BKC=180°﹣∠NKB﹣∠MKC=180°﹣(180°﹣∠ABK)﹣(180°﹣∠DCK)=∠ABK+∠DCK﹣180°,∴∠BKC=360°﹣2∠BHC﹣180°=180°﹣2∠BHC.
又∵∠BKC﹣∠BHC=33°,∴∠BHC=∠BKC﹣33°,∴∠BKC=180°﹣2(∠BKC﹣33°),∴∠BKC=82°.

故答案为:82°.

练习册系列答案
相关题目