题目内容
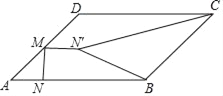
【题目】如图,在平行四边形ABCD中,∠A=45°,AB=4,AD=2![]() ,M是AD边的中点,N是AB边上一动点,将线段M绕点M逆时针旋转90至MN′,连接N′B,N′C,则N′B+N′C的最小值是_____.
,M是AD边的中点,N是AB边上一动点,将线段M绕点M逆时针旋转90至MN′,连接N′B,N′C,则N′B+N′C的最小值是_____.
【答案】![]()
【解析】
如图,作ME⊥AD交AB于E,连接EN′、AC、作CF⊥AB于F,根据已知可推知当A、N′、C共线时,N′B+N′C的值最小,最小值=AC,利用勾股定理救出AC的长即可得答案.
如图,作ME⊥AD交AB于E,连接EN′、AC、作CF⊥AB于F,
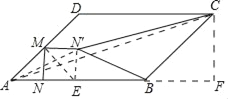
∵∠MAE=45°,
∴△MAE是等腰直角三角形,
∴MA=ME,
∵∠AME=∠NMN′=90°,
∴∠AMN=∠EMN′,
∵MN=MN′,
∴△AMN≌△EMN′,
∴∠MAN=∠MEN′=45°,
∴∠AEN′=90°,
∴EN′⊥AB,
∵AM=DM=![]() ,AB=4,
,AB=4,
∴AE=2,EB=2,
∴AE=EB,
∴N′B=N′A,
∴N′B+N′C=N′A+N′C,
∴当A、N′、C共线时,N′B+N′C的值最小,最小值=AC,
在Rt△BCF中,∵BC=AD=2![]() ,∠CBF=∠DAB=45°,
,∠CBF=∠DAB=45°,
∴CF=BF=2,
在Rt△ACF中,AC=![]() ,
,
故答案为:2![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目