题目内容
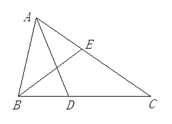
【题目】如图所示,点D在AC上,点E在AB上,且AB=AC,BC=BD,AD=DE=EB,求∠A的度数.

【答案】45°.
【解析】试题分析:由线段相等,可得对应角相等,通过转化,将∠A、∠ABC都与∠DBE建立联系,从而即可求解∠A的值.
试题解析:∵AB=AC,
∴∠ABC=∠C,又BC=BD,
∴∠BDC=∠C,
∵∠A+∠C+∠ABC=180°,∠DBC+∠C+∠BDC=180°,
∴∠DBC=∠A,
∵AD=DE=EB,
∴∠A=∠AED,∠EDB=∠EBD,
∴∠A=2∠DBE,即∠ABC=3∠DBE,
∵∠A+2∠C=180°,
∴2∠DBE+2∠ABC=180°,
∴2∠DBE+2×(3∠DBE)=180°,
即8∠DBE=180°,
∠A=2∠DBE=45°.

练习册系列答案
相关题目