题目内容
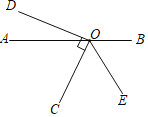
【题目】如图,点O在直线AB上,OC、OD是两条射线,OC⊥OD,射线OE平分∠BOC.
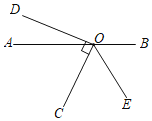
(1)若∠DOE=150°,求∠AOC的度数.
(2)若∠DOE=α,则∠AOC= .(请用含α的代数式表示)
【答案】(1)∠AOC=60°,(2)360°﹣2α.
【解析】
(1)利用垂直的定义和角的和差关系可得∠COE,由角平分线的性质可得∠BOE,然后根据平角的定义解答即可;
(2)根据垂直的定义和角的和差关系可得∠COE,由角平分线的性质可得∠BOE,然后利用平角的定义求解即可.
解:(1)∵OC⊥OD,∴∠DOC=90°,
∵∠DOE=150°,∴∠COE=∠DOE﹣∠COD=150°﹣90°=60°,
∵射线OE平分∠BOC,∴∠COE=∠BOE=60°,
∴∠AOC=180°﹣∠COE﹣∠BOE=180°﹣60°﹣60°=60°,
(2)∵OC⊥OD,∴∠DOC=90°,
∵∠DOE=α,∴∠COE=∠DOE﹣∠COD=α﹣90°,
∵射线OE平分∠BOC,∴∠COE=∠BOE=α﹣90°,
∴∠AOC=180°﹣∠COE﹣∠BOE=180°﹣(α﹣90°)﹣(α﹣90°)=360°﹣2α,
故答案为:360°﹣2α.

练习册系列答案
相关题目