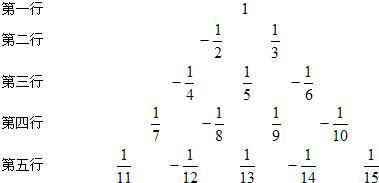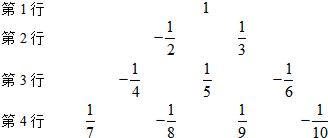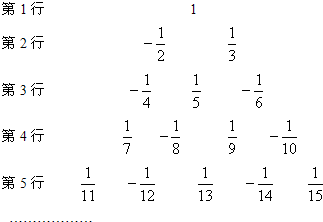题目内容
将1,-| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
第1行 1
第2行 -
| 1 |
| 2 |
| 1 |
| 3 |
第3行 -
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
第4行
| 1 |
| 7 |
| 1 |
| 8 |
| 1 |
| 9 |
| 1 |
| 10 |
…请写出第20行从左到右的第10个数是
分析:通过观察得出①每行从左起第1个数的分母可表示为:
,则可写出第20行的第1个数的分母,②第20行第10个数分母是第20行的第1个数的分母加9,③分母是奇数时为负数,偶数时为正数,且分子都为1,据以上规律求解.
| n2-n+2 |
| 2 |
解答:解:通过观察得:
第1行的第1个数的分母为:
=1,
第2行的第1个数的分母为:
=2,
第3行的第1个数的分母为:
=4,
第4行的第1个数的分母为:
=7,
…,
所以第20行的第1个数的分母为:
=191,
则第2行的第10个数的分母为:191+9=200,
所以第20行从左到右的第10个数是-
,
故答案为:-
.
第1行的第1个数的分母为:
| 12-1+2 |
| 2 |
第2行的第1个数的分母为:
| 22-2+2 |
| 2 |
第3行的第1个数的分母为:
| 32-3+2 |
| 2 |
第4行的第1个数的分母为:
| 42-4+2 |
| 2 |
…,
所以第20行的第1个数的分母为:
| 202-20+2 |
| 2 |
则第2行的第10个数的分母为:191+9=200,
所以第20行从左到右的第10个数是-
| 1 |
| 200 |
故答案为:-
| 1 |
| 200 |
点评:此题考查的知识点是数字的变化类问题,关键是通过观察得出每行从左起第1个数的分母可表示为:
.
| n2-n+2 |
| 2 |

练习册系列答案
相关题目
将1,-
,
,-
,
,-
,…,按一定规律排成下表:
从表中可以看到第四行中,自左向右第三个数是
;第五行自左向右第二个数是-
,那么第199行自左向右第8个数是 ,第2006行自左向右第11个数是 .
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 第1行 | 1 | ||||||||||
| 第2行 | -
| ||||||||||
| 第3行 | -
| ||||||||||
| 第4行 |
| ||||||||||
| 第5行 |
| ||||||||||
| … | … |
| 1 |
| 9 |
| 1 |
| 12 |