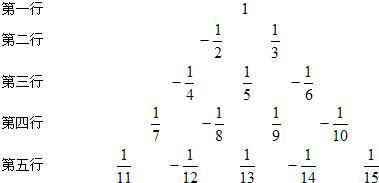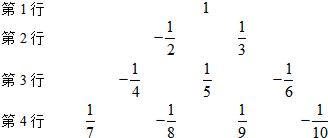题目内容
将1,-
,
,-
,
,-
,…按一定规律排列如下:
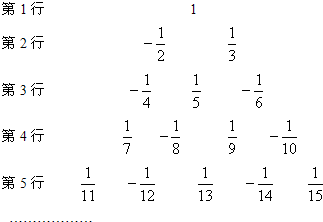
请你写出第40行从左至右第10个数是
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
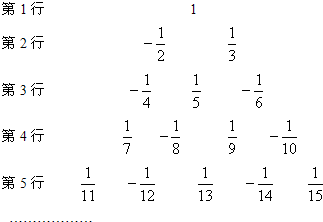
请你写出第40行从左至右第10个数是
-
| 1 |
| 790 |
-
.| 1 |
| 790 |
分析:观察各行的规律,分三部分分析:分数符号的规律,即当分母是奇数时,为正号.当分母是偶数时,符号是负号.所有的分子都是1.分母是从1开始连续的整数,第n行末尾的分母即是1+2+3+…+n=
.根据这一规律,计算第39行末尾数的分母是
=780,则第40行从左至右第10个数的分母是780+10=790,则该分数是-
.
| n(n+1) |
| 2 |
| 39×40 |
| 2 |
| 1 |
| 790 |
解答:解:∵分母是从1开始连续的整数,第n行末尾的分母即是1+2+3+…+n=
.
∴第39行末尾数的分母是
=780,
则第40行从左至右第10个数的分母是190+10=200
则该分数是-
.
故答案为:-
.
| n(n+1) |
| 2 |
∴第39行末尾数的分母是
| 39×40 |
| 2 |
则第40行从左至右第10个数的分母是190+10=200
则该分数是-
| 1 |
| 790 |
故答案为:-
| 1 |
| 790 |
点评:此题主要是分析分母的规律,根据分母的奇偶性确定该数的符号.本题的关键规律为:分母是从1开始连续的整数,第n行末尾的分母即是1+2+3+…+n=此题主要是分析分母的规律,根据分母的奇偶性确定该数的符号.本题的关键规律为:分母是从1开始连续的整数,第n行末尾的分母即是1+2+3+…+n=
.
| n(n+1) |
| 2 |

练习册系列答案
相关题目
将1,-
,
,-
,
,-
,…,按一定规律排成下表:
从表中可以看到第四行中,自左向右第三个数是
;第五行自左向右第二个数是-
,那么第199行自左向右第8个数是 ,第2006行自左向右第11个数是 .
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 6 |
| 第1行 | 1 | ||||||||||
| 第2行 | -
| ||||||||||
| 第3行 | -
| ||||||||||
| 第4行 |
| ||||||||||
| 第5行 |
| ||||||||||
| … | … |
| 1 |
| 9 |
| 1 |
| 12 |