题目内容
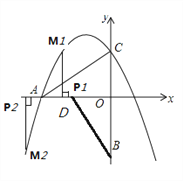
【题目】如图,把Rt△ACO以O点为中心,逆时针旋转90 ,得Rt△BDO,点B坐标为(0,-3),点C坐标为(0, ![]() ),,抛物线y=-
),,抛物线y=-![]() x2+bx+c经过点A和点C
x2+bx+c经过点A和点C
(1)求b,c的值;
(2)在x轴以上的抛物线对称轴上是否存在点Q,使得△ACQ为等腰三角形?若存在,直接写出点Q的坐标;若不存在,请说明理由
(3)点P从点O出发沿x轴向负半轴运动,每秒1个单位,过点P作y轴的平行线交抛物线于点M,当t为几秒时,以M、P、O、C为顶点得四边形是平行四边形?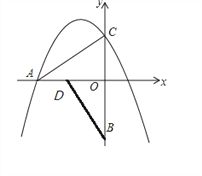
【答案】(1)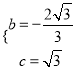 (2)存在,有2个Q点,坐标分别为:(—1,
(2)存在,有2个Q点,坐标分别为:(—1, ![]() );(—1,
);(—1, ![]() )(3)当t=2或
)(3)当t=2或![]() +1秒时,以M、P、O、C为顶点得四边形是平行四边形.
+1秒时,以M、P、O、C为顶点得四边形是平行四边形.
【解析】试题分析:(1)先由旋转得出点A的坐标为(—3,0),直接利用待定系数法求出抛物线解析式得出即可;
(2)利用当AQ=AC=![]() ,以及当AC=Q1C时,分别得出符合题意的答案即可;
,以及当AC=Q1C时,分别得出符合题意的答案即可;
(3)利用平行四边形的性质首先得出BC的长,进而表示出线段ME的长,进而求出答案.
(1) 由旋转知:OA=OB=3
∴A(—3,0)
由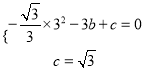 ,∴
,∴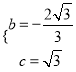 ……4分
……4分
(2)由(1)得y=-![]() x2+bx+c=-
x2+bx+c=-![]() x2
x2![]() x+
x+![]() =-
=-![]() x+1)2
x+1)2![]() ,即抛物线的对称轴为直线x=-1,
,即抛物线的对称轴为直线x=-1,
如图
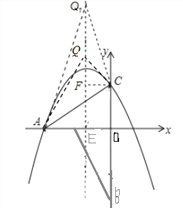
①当AC=AQ时,直线x=-1和x轴交于E点,AO=3,CO=![]() ,∴AC=
,∴AC=![]() ,AE=2,∴QE=
,AE=2,∴QE=![]() ,故Q的坐标为:(-1,
,故Q的坐标为:(-1, ![]() );
);
②当AC=Q1C时,过点C作CF⊥直线x=-1,于一点F,则FC=1,
∵AO=3,CO=![]() ,∴AC=
,∴AC=![]() ,∴Q1C=
,∴Q1C=![]() ,∴FQ1=
,∴FQ1=![]() ,故Q1的坐标为:(-1,
,故Q1的坐标为:(-1, ![]() );
);
所以存在2个Q点,坐标分别为:(—1, ![]() );(—1,
);(—1, ![]() ).
).
(3)∵OC=![]() ,当 M、P、O、C为顶点得四边形是平行四边形时,PM=
,当 M、P、O、C为顶点得四边形是平行四边形时,PM=![]()
∴M点的纵坐标为![]() 或-
或-![]() .
.
由![]()
解之,x=-2或0
由 ![]()
解之,x=-1+![]() 或-1-
或-1-![]()
结合条件及图形分析得:OP=2或![]() +1
+1
∴当t=2或![]() +1秒时,以M、P、O、C为顶点得四边形是平行四边形。
+1秒时,以M、P、O、C为顶点得四边形是平行四边形。

 中考解读考点精练系列答案
中考解读考点精练系列答案