题目内容
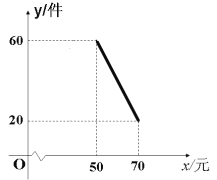
【题目】某商店试销一种新商品,该商品的进价为40元/件,经过一段时间的试销发现,每月的销售量会因售价在40~70元之间的调整而不同。当售价在40~50元时,每月销售量都为60件;当售价在50~70元时,每月销售量与售价的关系如图所示,令每月销售量为y件,售价为x元/件,每月的总利润为Q元。
(1)当售价在50~70元时,求每月销售量为y与x的函数关系式?
(2)当该商品售价x是多少元时,该商店每月获利最大,最大利润是多少元?
(3)若该商店每月采购这种新商品的进货款不低于1760元,则该商品每月最大利润为 元。
【答案】(1)y=—2x+160(50≤x≤70) ;(2)当该商品售价是60元时,该商店每月获利最大,最大利润是800元.(3)792元
【解析】试题分析:(1)由图象可知当售价在50~70元时,y与x满足一次函数的关系,可设y=kx+b(k≠0),把(50,60),,70,20)代入求出k、b的值即可;
(2)当40≤x≤50,Q=60x—2400,当50≤x≤70,Q=—2(x—60)2+800,在各自的自变量取值的范围内,由函数的增减性可求得各自的最大值,进行比较取大的一个值即可.
(3)由进货款不低于1760元,可得销售量≥44件,即—2x+160≥44,可得x≤58,再由每月利润Q=—2(x—60)2+800,可求得Q在50≤ x≤58的最大值.
试题解析:(1)令y=kx+b
由图知:当x=50时,y=60;当x=70时,y=20.
∴![]() ∴
∴![]()
∴y=—2x+160(50≤x≤70)
(2)由题可知,
当40≤x≤50
Q=60(x—40)=60x—2400
∵60>0, ∴Q随x的增大而增大,
∴x=50时,Q有最大值600元.
当50≤x≤70
Q=y(x—40)=2x2+240x—6400=—2(x—60)2+800
∵—2<0, ∴x=60时,Q有最大值800元.
综上所述,当该商品售价是60元时,该商店每月获利最大,最大利润是800元.
(3)根据题意,得40y≥1760,即y≥44,
所以-2x+160≥44,解得x≤58,
Q=-2(x-60)2+800,
因为-2<0,在对称轴x=60左侧,y随x的增大而增大,
所以当x=58时,Q有最大值,最大值为-2(58-60)2+800=792.

 名校课堂系列答案
名校课堂系列答案