题目内容
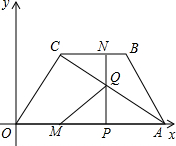
四边形OABC是等腰梯形,OA∥BC.在建立如图的平面直角坐标系中,A(4,0),B(3,2),点M从O点以每秒2个单位的速度向终点A运动;同时点N从B点出发以每秒1个单位的速度向终点C运动,过点N作NP垂直于x轴于P点连接AC交NP于Q,连接MQ.
(1)写出C点的坐标;
(2)若动点N运动t秒,求Q点的坐标;(用含t的式子表示)
(3)其△AMQ的面积S与时间t的函数关系式,并写出自变量t的取值范围;
(4)当t取何值时,△AMQ的面积最大;
(5)当t为何值时,△AMQ为等腰三角形.
(1)写出C点的坐标;
(2)若动点N运动t秒,求Q点的坐标;(用含t的式子表示)
(3)其△AMQ的面积S与时间t的函数关系式,并写出自变量t的取值范围;
(4)当t取何值时,△AMQ的面积最大;
(5)当t为何值时,△AMQ为等腰三角形.

(1)C(1,2).
(2)过C作CE⊥x轴于E,则CE=2
当动点N运动t秒时,NB=t
∴点Q的横坐标为3-t
设Q点的纵坐标为yQ
由PQ∥CE得
=
∴yQ=
∴点Q(3-t,
);
(3)点M以每秒2个单位运动,
∴OM=2t,AM=4-2t,
S△AMQ=
AM•PQ=
•(4-2t)•
=
(2-t)(t+1)
=-
(t2-t-2)
当t=2时,M运动到A点,△AMQ不存在,
∴t≠2,
∴t的取值范围是0≤t<2;
(4)由S△AMQ=-
(t2-t-2)=-
(t-
)2+
.
当t=
时,Smax=
;
(5)①若QM=QA
∵QP⊥OA,
∴MP=AP,
而MP=4-(1+t+2t)=3-3t,
即1+t=3-3t,
t=
,
∴当t=
时,△QMA为等腰三角形;
②若AQ=AM
AQ2=AP2+PQ2=(1+t)2+(
)2=
(1+t)2AQ=
,
AM=4-2t
(1+t)=4-2t,
t=
而0<
<2,
∴当t=
时,△QMA为等腰三角形;
③若MQ=MA
MQ2=MP2+PQ2
=(3-3t)2+(
)2=
t2-
t+
∴
t2-
t+
=(4-2t)2
t2-
t-
=0
解得t=
或t=-1(舍去)
∵0<
<2,
∴当t=
时,△QMA为等腰三角形;
综上所述:当t=
,t=
或t=
△QMA都为等腰三角形.
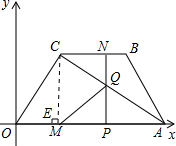
(2)过C作CE⊥x轴于E,则CE=2
当动点N运动t秒时,NB=t
∴点Q的横坐标为3-t
设Q点的纵坐标为yQ
由PQ∥CE得
| yQ |
| 2 |
| 1+t |
| 3 |
∴yQ=
| 2+2t |
| 3 |
∴点Q(3-t,
| 2+2t |
| 3 |
(3)点M以每秒2个单位运动,
∴OM=2t,AM=4-2t,
S△AMQ=
| 1 |
| 2 |
| 1 |
| 2 |
| 2+2t |
| 3 |
=
| 2 |
| 3 |
=-
| 2 |
| 3 |
当t=2时,M运动到A点,△AMQ不存在,
∴t≠2,
∴t的取值范围是0≤t<2;
(4)由S△AMQ=-
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
当t=
| 1 |
| 2 |
| 3 |
| 2 |
(5)①若QM=QA
∵QP⊥OA,
∴MP=AP,
而MP=4-(1+t+2t)=3-3t,
即1+t=3-3t,
t=
| 1 |
| 2 |
∴当t=
| 1 |
| 2 |
②若AQ=AM
AQ2=AP2+PQ2=(1+t)2+(
| 2+2t |
| 3 |
| 13 |
| 9 |
| ||
| 3 |
AM=4-2t
| ||
| 3 |
t=
85-18
| ||
| 23 |
85-18
| ||
| 23 |
∴当t=
85-18
| ||
| 23 |
③若MQ=MA
MQ2=MP2+PQ2
=(3-3t)2+(
| 2+2t |
| 3 |
| 85 |
| 9 |
| 154 |
| 9 |
| 85 |
| 9 |
∴
| 85 |
| 9 |
| 154 |
| 9 |
| 85 |
| 9 |
=(4-2t)2
| 49 |
| 9 |
| 10 |
| 9 |
| 59 |
| 9 |
解得t=
| 59 |
| 49 |
∵0<
| 59 |
| 49 |
∴当t=
| 59 |
| 49 |
综上所述:当t=
| 1 |
| 2 |
85-18
| ||
| 23 |
| 59 |
| 49 |


练习册系列答案
相关题目
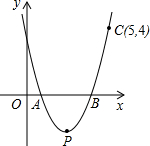
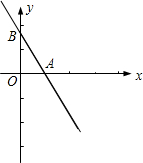 于点B,tan∠OAB=
于点B,tan∠OAB= 60°.飞机继续飞行0.1千米到达E处进行空投,已知空投物资在空中下落过程中的轨迹是抛物线,若要使空投物资刚好落在O处.
60°.飞机继续飞行0.1千米到达E处进行空投,已知空投物资在空中下落过程中的轨迹是抛物线,若要使空投物资刚好落在O处.