题目内容
【题目】如图,已知直线a // b,点A、E在直线a上,点B、F在直线b上,∠ABC=100°,BD平分∠ABC交直线a于点D,线段EF在线段AB的左侧.若将线段EF沿射线 AD的方向平移,在平移的过程中BD所在的直线与 EF所在的直线交于点P.试探索 ∠1的度数与∠EPB的度数有怎样的关系?

为了解决以上问题,我们不妨从EF的某些特殊位置研究,最后再进行一般化.
(特殊化)
(1)如图,当∠1=40°,且点P在直线a、b之间时,求∠EPB的度数;

(2)当∠1=70 °时,求∠EPB的度数;

(一般化)
(3)当∠1=n°时,求∠EPB的度数.(直接用含n的代数式表示)
【答案】(1)170°(2)见解析(3)①见解析②见解析
【解析】
(1)作PG∥a,根据平行线性质和角平分线性质可得∠GPB=180°-![]() ∠ABC=130°,计算即可;(2)作PG∥a,结合画图,分3种情况当交点P在直线a上方,∠EPB=20°;当交点P在直线a、b之间,∠EPB=160°;当交点P在直线b下方,∠EPB=20°;(3)根据(1)(2)情况,分2种情况①当n>50°时;②当n<50°时,各有3种情况.
∠ABC=130°,计算即可;(2)作PG∥a,结合画图,分3种情况当交点P在直线a上方,∠EPB=20°;当交点P在直线a、b之间,∠EPB=160°;当交点P在直线b下方,∠EPB=20°;(3)根据(1)(2)情况,分2种情况①当n>50°时;②当n<50°时,各有3种情况.
(1)作PG∥a,
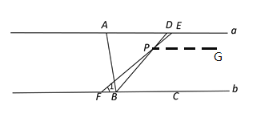
∴∠EPG=∠EFC=400
∵a∥b
∴PG∥b
∴∠GPB+∠CBD=1800
又∵BD是∠ABC平分线,且∠ABC=1000,
∴∠GPB=1800-![]() ∠ABC=1300
∠ABC=1300
∴∠EPB=∠EPG+∠GPB=1700
(2)①当交点P在直线a上方,作PG∥a,
∵a∥b
∴PG∥b
∴∠EPG=∠1, ∠GPB=∠DBC
∴∠EPB=700-500=200
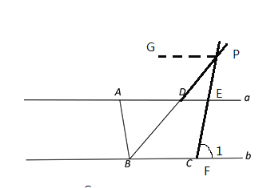
②当交点P在直线a、b之间,作PG∥a,

∵a∥b
∴PG∥b
∴∠GPB=∠PBC=![]() ∠ABC=500,∠BFE=∠EPG=1800-∠1
∠ABC=500,∠BFE=∠EPG=1800-∠1
∴∠EPB=∠EPG+∠GPB=500+1800-∠1=2300-700=1600
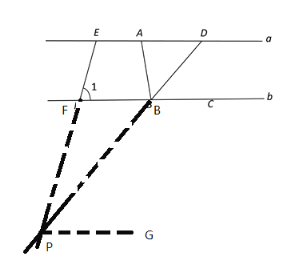
③当交点P在直线b下方,作PG∥a,
∵a∥b
∴PG∥b
∴∠EPG=∠1, ∠GPB=∠DBC
∴∠EPB=700-500=200
(3)由(1)(2)得:①当n>500时,
交点P在直线a上方,∠EPB=n-500
交点P在直线a、b之间,∠EPB=2300-n
交点P在直线b下方,∠EPB=n-500
②当n<500时,
交点P在直线a上方,∠EPB=500-n
交点P在直线a、b之间,∠EPB=1300+n
交点P在直线b下方,∠EPB=500-n

 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案

