题目内容
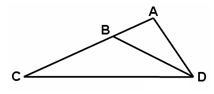
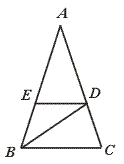
已知:如图,在Rt△ABC中,∠C=90°, D、E分别为AB、 AC边上的点,且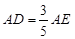 ,连结DE.若AC=3,AB=5,猜想DE与AB有怎样的位置关系?并证明你的结论.(4分)
,连结DE.若AC=3,AB=5,猜想DE与AB有怎样的位置关系?并证明你的结论.(4分)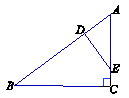
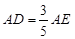 ,连结DE.若AC=3,AB=5,猜想DE与AB有怎样的位置关系?并证明你的结论.(4分)
,连结DE.若AC=3,AB=5,猜想DE与AB有怎样的位置关系?并证明你的结论.(4分)
∵垂直提示:证△ADE∽△ACB
考点:相似三角形的判定与性质.
分析:根据△ADE与△ACB两边对应成比例及一夹角相等,证明两三角形相似,然后利用相似三角形的性质即可得到∠ADE=∠C=90°,从而得到DE与AB的位置关系是互相垂直.
解答:猜想:DE与AB的位置关系是互相垂直.
证明:∵AC=3,AB=5,AD=
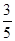 AE,
AE,∴
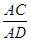 =
=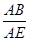 .
.∵∠A=∠A,
∴△ADE∽△ACB.
∵∠C=90°,
∴∠ADE=∠C=90°.
∴DE⊥AB.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
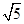 ;
;
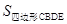 = 。
= 。

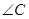 为直角,
为直角,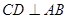 于
于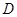 ,
,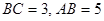 , DB = , CD =
, DB = , CD = 
 ,
,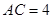 ,
,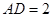 ,
,