题目内容
如图△ABC中,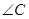 为直角,
为直角,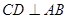 于
于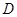 ,
,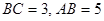 , DB = , CD =
, DB = , CD = 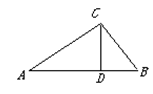
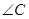 为直角,
为直角,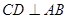 于
于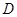 ,
,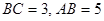 , DB = , CD =
, DB = , CD = 
 ,
,
分析:由△ABC中,∠C为直角,CD⊥AB,根据等角的余角相等,即可求得∠BCD=∠A,又由BC=3,AB=5,利用勾股定理即可求得AC的长,然后在Rt△BCD中,利用三角函数的知识即可求得答案.
解:∵CD⊥AB,
∴∠CDB=90°,
∴∠B+∠BCD=90°,
∵△ABC中,∠C为直角,
∴∠A+∠B=90°,
∴∠A=∠BCD,
∵BC=3,AB=5,
∴AC=
 =4,
=4,在Rt△BCD中,DB=BC?sin∠BCD=BC?sin∠A=3×
 =
= ;
;CD=BC?cos∠BCD=BC?cos∠A=3×
 =
= .
.故答案为:
 ,
, .
.
练习册系列答案
相关题目
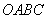 沿
沿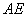 折叠,使点
折叠,使点 恰好落在
恰好落在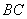 上
上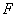 处,以
处,以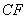 为边作正方形
为边作正方形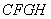 ,延长
,延长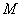 ,使
,使 ,再以
,再以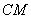 、
、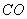 为边作矩形
为边作矩形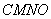 .
.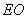 、
、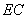 的大小,并说明理由.
的大小,并说明理由.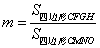 ,请问
,请问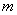 是否为定值?若是,请求出
是否为定值?若是,请求出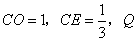 为
为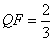 ,抛物线
,抛物线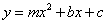 经过
经过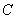 、
、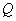 两点,请求出此抛物线的解析式.
两点,请求出此抛物线的解析式.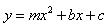 与线段
与线段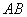 交于点
交于点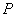 ,试问在直线
,试问在直线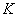 ,使得以
,使得以 、
、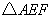 相似?若存在,请求直线
相似?若存在,请求直线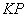 与
与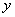 轴的交点
轴的交点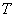 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
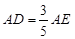 ,连结DE.若AC=3,AB=5,猜想DE与AB有怎样的位置关系?并证明你的结论.(4分)
,连结DE.若AC=3,AB=5,猜想DE与AB有怎样的位置关系?并证明你的结论.(4分)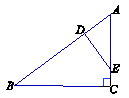
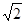 ︰1
︰1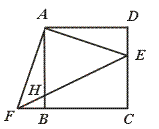
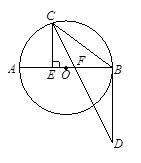
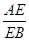 =
=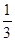 ,则
,则 的值为 【 】
的值为 【 】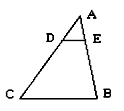
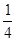 C、
C、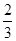 D、
D、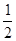
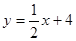 的图象与该二次函数的图象交于
的图象与该二次函数的图象交于 点(8,8),直线与
点(8,8),直线与 轴的交点为C,与y轴的交点为B.
轴的交点为C,与y轴的交点为B.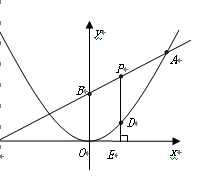
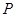 为线段
为线段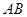 上的一个动点(点
上的一个动点(点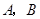 不重合),过
不重合),过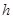 ,点
,点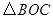 相似?若存在,请求出
相似?若存在,请求出