题目内容
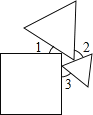
【题目】操作：某数学兴趣小组在研究用一副三角板拼角时，小明、小亮分别拼出图1、图2所示的两种图形，如图1，小明把30°和90°的角按如图1方式拼在一起；小亮把30°和90°的角按如图2方式拼在一起，并在各自所拼的图形中分别作出∠AOB、∠COD的平分线OE、OF．小明很容易地计算出图1中∠EOF=60°．
计算：请你计算出图2中∠EOF= 度．
归纳：通过上面的计算猜一猜，当有公共顶点的两个角∠α、∠β有一条边重合，且这两个角在公共边的异侧时，则这两个角的平分线所夹的角= ．（用含α、β的代数式表示）
拓展：小明把图1中的三角板AOB绕点O顺时针旋转90°后得到图3，小亮把图2中的三角板AOB绕点O顺时针旋转90°后得到图4（两图中的点O、B、D在同一条直线上）．在图3中，易得到∠EOF=∠DOF﹣∠BOE=
∠COD﹣
∠AOB=45°﹣15°=30°；仿照图3的作法，请你通过计算，求出图4中∠EOF的度数（写出解答过程）．
反思：通过上面的拓展猜一猜，当有公共顶点的两个角∠α、∠β（∠α＞∠β）有一条边重合，且这两个角在公共边的同侧时，则这两个角的平分线所夹的角= ．
【答案】
【解析】
试题分析：计算和归纳：根据角平分线的定义和角的位置关系可以求得：∠AOE=∠EOB=
∠AOB，∠COF=∠FOD=∠COD，再根据∠EOF=∠EOB+∠BOF可以求得∠EOF的度数；拓展和反思：根据角平分线的定义和角的位置关系可以求得：∠AOE=∠EOB=∠AOB，∠COF=∠FOD=∠COD，再根据∠EOF=∠BOF﹣∠BOE可以求得∠EOF的度数．
解：计算：∵∠AOC=60°，∠COD=90°，
∵OE、OF分别平分∠AOB、∠COD，
∴∠AOE=∠EOB=∠AOB，∠COF=∠FOD=∠COD，
∴∠EOF=∠BOE+∠COF=75°，
故答案为：75°；
归纳：
；
故答案为：
；
拓展：∵OE、OF分别平分∠AOB、∠COD，
∴
=30°，
，
∴∠EOF=∠DOF﹣∠DOE=15°；
反思：，
故答案为：．
