ЬтФПФкШн
ЁОЬтФПЁП2016ФъЙњМЪТэРЫЩШќгкГаЕТЪаОйАьЃЌЦ№ЕуГаЕТЪаЪЈзгдАЃЌШќЕРЮЊЭтЛЗТЗЃЌжеЕуЮЊАТЬхжааФЃЈШќЕРЛљБОЮЊжБЯпЃЉЃЎдкШќЕРЩЯгаAЃЌBСНИіЗўЮёЕуЃЌЯжгаМзЃЌввСНИіЗўЮёШЫдБЃЌЗжБ№ДгAЃЌBСНИіЗўЮёЕуЭЌЪБГіЗЂЃЌбижБЯпдШЫйХмЯђжеЕуCЃЈАТЬхжааФЃЉЃЌШчЭМ1ЫљЪОЃЌЩшМзЁЂввСНШЫГіЗЂxhКѓЃЌгыBЕуЕФОрРыЗжБ№ЮЊyМзkmЁЂyввkmЃЌyМзЁЂyввгыxЕФКЏЪ§ЙиЯЕШчЭМ2ЫљЪОЃЎ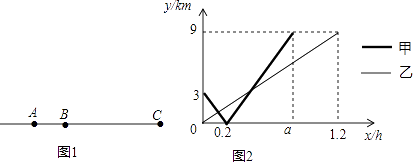
ЃЈ1ЃЉДгЗўЮёЕуAЕНжеЕуCЕФОрРыЮЊkmЃЌa=hЃЛ
ЃЈ2ЃЉЧѓМзввЯргіЪБxЕФжЕЃЛ
ЃЈ3ЃЉМзввСНШЫжЎМфЕФОрРыгІВЛГЌЙ§1kmЪБЃЌГЦЮЊзюМбЗўЮёОрРыЃЌДгМзЁЂввЯргіЕНМзЕНДяжеЕувдЧАЃЌБЃГжзюМбЗўЮёОрРыЕФЪБМфгаЖрГЄЃП
ЁОД№АИЁП
ЃЈ1ЃЉ12,0.8
ЃЈ2ЃЉНтЃКЩшввЖдгІЕФКЏЪ§НтЮіЪНЮЊЃКy=kxЃЌ
1.2k=9ЃЌЕУk=7.5ЃЌ
МДввЖдгІЕФКЏЪ§НтЮіЪНЮЊЃКy=7.5xЃЌ
ЕБxЃО0.2ЪБЃЌЩшМзЖдгІЕФКЏЪ§НтЮіЪНЮЊy=mx+nЃЌ
![]() ЃЌЕУ
ЃЌЕУ ![]() ЃЌ
ЃЌ
МДЕБxЃО0.2ЪБЃЌМзЖдгІЕФКЏЪ§НтЮіЪНЮЊy=15xЉ3ЃЌ
Сю7.5x=15xЉ3ЃЌЕУx=0.4ЃЌ
МДМзввЯргіЪБxЕФжЕЪЧ0.4
ЃЈ3ЃЉНтЃКгЩЬтвтПЩЕУЃЌ
15xЉ3Љ7.5xЁм1ЃЌЕУxЁм ![]() ЃЌ
ЃЌ
Ёп ![]() ЃЌ
ЃЌ
ЁрМзЁЂввЯргіЕНМзЕНДяжеЕувдЧАЃЌБЃГжзюМбЗўЮёОрРыЕФЪБМфга ![]() h
h
ЁОНтЮіЁПНтЃКЃЈ1ЃЉгЩЭМЯѓПЩЕУЃЌ
ДгЗўЮёЕуAЕНжеЕуCЕФОрРыЮЊЃК3+9=12ЃЈkmЃЉЃЌ
a=0.2+9ЁТЃЈ3ЁТ0.2ЃЉ=0.8ЃЌ
ЫљвдД№АИЪЧЃК12ЃЌ0.8ЃЛ
ЁОПМЕуОЋЮіЁПНтД№ДЫЬтЕФЙиМќдкгкРэНтШЗЖЈвЛДЮКЏЪ§ЕФБэДяЪНЕФЯрЙижЊЪЖЃЌеЦЮеШЗЖЈвЛИівЛДЮКЏЪ§ЃЌашвЊШЗЖЈвЛДЮКЏЪ§ЖЈвхЪНy=kx+bЃЈkВЛЕШгк0ЃЉжаЕФГЃЪ§kКЭbЃЎНтетРрЮЪЬтЕФвЛАуЗНЗЈЪЧД§ЖЈЯЕЪ§ЗЈЃЎ