题目内容
已知二次函数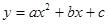
的图象如图，其对称轴x＝－1，给出下列结果
①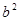
＞4ac，②abc＞0，③2a＋b＝0，④a＋b＋c＞0，⑤a－b＋c＜0，则正确的结论是（ ）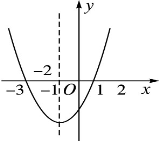
| A．①②③④ | B．②④⑤ | C．②③④ | D．①④⑤ |
D．
解析试题分析：∵抛物线与x轴有两个交点，
∴b2﹣4ac＞0，即b2＞4ac＞，所以①正确；
∵抛物线开口向上，
∴a＞0，
∵对称轴为直线x=﹣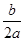
＜0，
∴b＞0，
∵抛物线与y轴的交点在x轴下方，
∴c＜0，
∴abc＜0，所以②错误；
又∵对称轴为直线x=﹣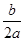=﹣1，
∴2a﹣b=0，所以③错误；
∵根据图像知，当x=1时，y>0，
∴a＋b＋c＞0，所以④正确；
∵根据图像知，当x=－1时，y<0，
∴a－b＋c＜0，所以⑤正确．
故选D．
考点：二次函数图象与系数的关系．
练习册系列答案
精英口算卡系列答案
应用题点拨系列答案
状元及第系列答案
同步奥数系列答案
相关题目
苏科版教材中有这样一句话：“一般地，如果二次函数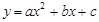
的图象与x轴有两个公共点，那么一元二次方程
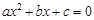有两个不相等的实数根．”据此判断方程x2－2x＝
－2实数根的情况是 ( )
| A．有三个实数根 | B．有两个实数根 | C．有一个实数根 | D．无实数根 |
对于二次函数y=2(x＋1)(x－3)，下列说法正确的是（ ）
| A．图象的开口向下 |
| B．当x＞1时，y随x的增大而减小 |
| C．当x＜1时，y随x的增大而减小 |
| D．图象的对称轴是直线x=－1 |
把抛物线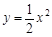
向左平移3个单位，再向下平移2个单位后，所得的抛物线的表达式是
A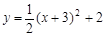． | B． |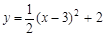
C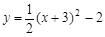． | D． |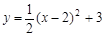
已知二次函数y＝a(x＋1)2－b(a≠0)有最小值，则a，b的大小关系为 ( )
| A．a>b | B．a<b |
| C．a＝b | D．不能确定 |
将二次函数y＝x2的图象向下平移一个单位，则平移以后的二次函数的解析式为( )
| A．y＝x2－1 | B．y＝x2＋1 |
| C．y＝(x－1)2 | D．y＝(x＋1)2 |
将进货单价为70元的某种商品按零售价100元一个售出时，每天能卖出20个，若这种商品的零售价在一定范围内每降价1元，其日销量就增加1个，为了获取最大利润则应降价
| A．20元 | B．15元 |
| C．10元 | D．5元 |
将二次函数y=3（x+2）2-4的图象向右平移3个单位，再向上平移1个单位，所得的图象的函数关系式是
| A．y=3（x+5）2-5 | B．y=3（x-1）2-5 |
| C．y=3（x-1）2-3 | D．y=3（x+5）2-3 |