题目内容
苏科版教材中有这样一句话：“一般地，如果二次函数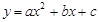
的图象与x轴有两个公共点，那么一元二次方程
有两个不相等的实数根．”据此判断方程x2－2x＝
－2实数根的情况是 ( )
| A．有三个实数根 | B．有两个实数根 | C．有一个实数根 | D．无实数根 |
C.
解析试题分析：将方程变形-1=（x-1）2，
设y1=-1，y2=（x-1）2，在坐标系中画出两个函数的图象如图所示：
可看出两个函数有一个交点（1，0）．
故方程x2-2x=-2有一个实数根．
故选C.
考点：抛物线与x轴的交点．
练习册系列答案
优质课堂快乐成长系列答案
相关题目
抛物线y=(x-1)2+2的顶点坐标是
| A．(1，-2) | B．(1，2) | C．(-1，2) | D．(-1，-2) |
已知0≤x≤
，那么函数y=﹣2x2+8x﹣6的最大值是（ ）
| A．﹣10.5 | B．2 | C．﹣2.5 | D．﹣6 |
CPD 的面积为y. 则下列图象中，能表示y与x的函数关系的图象大致是（ ）
B. 
C. 
D.
已知关于x的二次函数y＝x2－2x＋c的图像上有两点A(x1，y1)，B(x2，y2)，若x1<1<x2且x1＋x2＝2，则y1与y2的大小关系是
| A．y1<y2 | B．y1>y2 | C．y1＝y2 | D．不能确定 |
将二次函数
化为
的形式，结果为（ ）
A． | B． |
C． | D． |
已知二次函数
的图象如图，其对称轴x＝－1，给出下列结果
①
＞4ac，②abc＞0，③2a＋b＝0，④a＋b＋c＞0，⑤a－b＋c＜0，则正确的结论是（ ）
| A．①②③④ | B．②④⑤ | C．②③④ | D．①④⑤ |