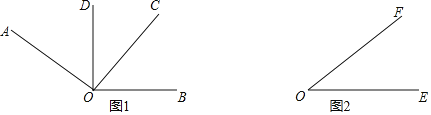ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩΡ≥ΑύΓΑ ΐ―ß–Υ»Λ–ΓΉιΓ±Ε‘Κ· ΐ![]() ΒΡΆΦœσΚΆ–‘÷ Ϋχ––ΝΥΧΫΨΩΘ§Ιΐ≥Χ»γœ¬Θ§«κ≤Ι≥δΆξ’ϊ.
ΒΡΆΦœσΚΆ–‘÷ Ϋχ––ΝΥΧΫΨΩΘ§Ιΐ≥Χ»γœ¬Θ§«κ≤Ι≥δΆξ’ϊ.
Θ®1Θ©Ή‘±δΝΩ![]() ΒΡ»Γ÷ΒΖΕΈß «»ΪΧε Β ΐΘ§
ΒΡ»Γ÷ΒΖΕΈß «»ΪΧε Β ΐΘ§![]() ”κ
”κ![]() ΒΡΦΗΉιΕ‘”Π÷ΒΝ–±μ»γœ¬ΘΚ
ΒΡΦΗΉιΕ‘”Π÷ΒΝ–±μ»γœ¬ΘΚ
| Γ≠ |
|
|
| 0 | 1 | 2 | 3 | 4 | 5 | Γ≠ |
| Γ≠ | 4 |
| 2 | 1 | 0 | 1 | 2 | 3 | 4 | Γ≠ |
Τδ÷–Θ§![]() __________.
__________.
Θ®2Θ©ΗυΨί…œ±μΒΡ ΐΨίΘ§‘Ύ»γΆΦΥυ ΨΒΡΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–ΟηΒψΘ§≤ΔΜ≠≥ωΝΥΚ· ΐΆΦœσΒΡ“Μ≤ΩΖ÷Θ§«κΜ≠≥ωΗΟΚ· ΐΆΦœσΒΡΝμ“Μ≤ΩΖ÷.
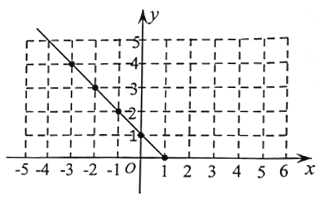
Θ®3Θ©Ιέ≤λΆΦœσΘ§–¥≥ωΗΟΚ· ΐΒΡΝΫΧθ–‘÷ ΘΚ
ΔΌ____________________________________________________________
ΔΎ____________________________________________________________
Θ®4Θ©Ϋχ“Μ≤ΫΧΫΨΩΚ· ΐΆΦœσΖΔœ÷ΘΚ
ΔΌΖΫ≥Χ![]() ΒΡΫβ «__________.
ΒΡΫβ «__________.
ΔΎΖΫ≥Χ![]() ΒΡΫβ «__________.
ΒΡΫβ «__________.
ΔέΙΊ”Ύ![]() ΒΡΖΫ≥Χ
ΒΡΖΫ≥Χ![]() ”–ΝΫΗω≤ΜœύΒ» Β ΐΗυΘ§‘ρ
”–ΝΫΗω≤ΜœύΒ» Β ΐΗυΘ§‘ρ![]() ΒΡ»Γ÷ΒΖΕΈß «__________.
ΒΡ»Γ÷ΒΖΕΈß «__________.
ΓΨ¥πΑΗΓΩΘ®1Θ©3ΘΜΘ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©ΔΌΚ· ΐ÷ΒyΓί0Κ· ΐ÷ΒyΓί0ΘΜΔΎΒ±xΘΨ1 ±Θ§yΥφxΒΡ‘ω¥σΕχ‘ω¥σΘΜΘ®4Θ©ΔΌ![]() ΘΜΔΎ
ΘΜΔΎ![]() Μρ
Μρ![]() ΘΜΔέ
ΘΜΔέ![]() .
.
ΓΨΫβΈωΓΩ
Θ®1Θ©«σ≥ωx=-2 ±ΒΡΚ· ΐ÷ΒΦ¥Ω…ΘΜ
Θ®2Θ©άϊ”ΟΟηΒψΖ®Μ≠≥ωΚ· ΐΆΦœσΦ¥Ω…ΘΜ
Θ®3Θ©ΫαΚœΆΦœσ–¥≥ωΝΫΗω–‘÷ Φ¥Ω…ΘΜ
Θ®4Θ©Ζ÷±π«σ≥ωΖΫ≥ΧΒΡΫβΦ¥Ω…ΫβΨωΈ ΧβΘΜ
ΫβΘΚΘ®1Θ©x=-2 ±Θ§y=|x-1|=3Θ§Ι m=3Θ§Ι ¥πΑΗΈΣ3Θ°
Θ®2Θ©Κ· ΐΆΦœσ»γΆΦΥυ ΨΘΚ
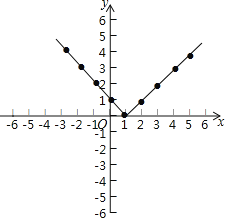
Θ®3Θ©ΔΌΚ· ΐ÷ΒyΓί0Θ§ΔΎΒ±xΘΨ1 ±Θ§yΥφxΒΡ‘ω¥σΕχ‘ω¥σΘΜ
Ι ¥πΑΗΈΣΚ· ΐ÷ΒyΓί0ΘΜΒ±xΘΨ1 ±Θ§yΥφxΒΡ‘ω¥σΕχ‘ω¥σΘΜ
Θ®4Θ©ΔΌΖΫ≥Χ|x-1|=0ΒΡΫβ «x=1
ΔΎΖΫ≥Χ|x-1|=1.5ΒΡΫβ «x=2.5Μρ-0.5
ΔέΙΊ”ΎxΒΡΖΫ≥Χ|x-1|=a”–ΝΫΗω Β ΐΗυΘ§‘ρaΒΡ»Γ÷ΒΖΕΈß «aΘΨ0Θ§
Ι ¥πΑΗΈΣx=1Θ§x=2.5Μρ-0.5Θ§aΘΨ0Θ°

 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗΓΨΧβΡΩΓΩ»γ±μ «“ΜΗω4ΓΝ4Θ®4––4Ν–Ι≤16ΗωΓΑ ΐΓ±Ήι≥…Θ©ΒΡΤφΟνΖΫ’σΘ§¥”’βΗωΖΫ’σ÷–―ΓΥΡΗωΓΑ ΐΓ±Θ§Εχ«“’βΥΡΗωΓΑ ΐΓ±÷–ΒΡ»ΈΚΈΝΫΗω≤Μ‘ΎΆ§“Μ––Θ§“≤≤Μ‘ΎΆ§“ΜΝ–Θ§”–ΚήΕύ―ΓΖ®Θ§Α―ΟΩ¥Έ―Γ≥ωΒΡΥΡΗωΓΑ ΐΓ±œύΦ”Θ§ΤδΚΆ «Ε®÷ΒΘ§‘ρΖΫ’σ÷–ΒΎ»ΐ––»ΐΝ–ΒΡΓΑ ΐΓ± «Θ®ΓΓΓΓΘ©
30 |
| 2 | 22 |
©¹3 | ©¹2 | ©¹ | 0 |
|©¹5| | 6 | 23 | |
Θ® | 4 |
| Θ® |
A. 5 B. 6 C. 7 D. 8