题目内容
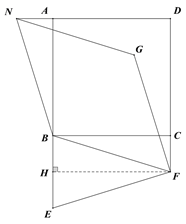
【题目】如图,已知正方形ABCD,E是AB延长线上一点,F是DC延长线上一点,且满足BF=EF,将线段EF绕点F顺时针旋转90°得FG,过点B作FG的平行线,交DA的延长线于点N,连接NG.

求证:BE=2CF;
试猜想四边形BFGN是什么特殊的四边形,并对你的猜想加以证明.
【答案】详见解析.
【解析】试题分析:(1)过F作FH⊥BE于点H,可证明四边形BCFH为矩形,可得到BH=CF,且H为BE中点,可得BE=2CF;
(2)由条件可证明△ABN≌△HFE,可得BN=EF,可得到BN=GF,且BN∥FG,可证得四边形BFGN为菱形.
试题解析:
证明:过F作FH⊥BE于H点,
在四边形BHFC中,∠BHF=∠CBH=∠BCF=90°,
所以四边形BHFC为矩形,
∴CF=BH,
∵BF=EF,FH⊥BE,
∴H为BE中点,
∴BE=2BH,
∴BE=2CF;
猜想:四边形BFGN是菱形.
证明:
∵将线段EF绕点F顺时针旋转90°得FG,
∴EF=GF,∠GFE=90°,
∴∠EFH+∠BFH+∠GFB=90°
∵BN∥FG,
∴∠NBF+∠GFB=180°,
∴∠NBA+∠ABC+∠CBF+∠GFB=180°,
∵∠ABC=90°,
∴∠NBA+∠CBF+∠GFB=180°90°=90°,
由BHFC是矩形可得BC∥HF,∴∠BFH=∠CBF,
∴∠EFH=90°∠GFB∠BFH=90°∠GFB∠CBF=∠NBA,
由BHFC是矩形可得HF=BC,
∵BC=AB,∴HF=AB,
在△ABN和△HFE中, 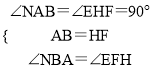 ,
,
∴△ABN≌△HFE,
∴NB=EF,
∵EF=GF,
∴NB=GF,
又∵NB∥GF,
∴NBFG是平行四边形,
∵EF=BF,∴NB=BF,
∴平行四边NBFG是菱形.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案【题目】某自行车厂计划每天生产![]() 辆自行车,但由于各种原因,实际每天生产量与计划生产量相比有所差异,下表是该厂某一周的实际生产情况(以计划产量为标准,超产记为正数,不足记为负数.单位:辆):
辆自行车,但由于各种原因,实际每天生产量与计划生产量相比有所差异,下表是该厂某一周的实际生产情况(以计划产量为标准,超产记为正数,不足记为负数.单位:辆):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与标准产量的差 |
|
|
|
|
|
|
|
(![]() )根据表格,这一周该厂实际生产自行车多少辆?
)根据表格,这一周该厂实际生产自行车多少辆?
(![]() )若该厂实行“每日计件工资制”,每生产一辆自行车可得
)若该厂实行“每日计件工资制”,每生产一辆自行车可得![]() 元,若超额完成任务,则超出部分每辆额外奖励
元,若超额完成任务,则超出部分每辆额外奖励![]() 元;若未完成任务,则每少生产一辆扣
元;若未完成任务,则每少生产一辆扣![]() 元,那么该厂工人这一周的工资总额是多少元?
元,那么该厂工人这一周的工资总额是多少元?
(![]() )若将(
)若将(![]() )中的“每日计件工资制”改为“每周计件工资制”,其他条件不变,在此方式下该厂工人一周的工资总额与“每日计件工资制”相比是减少还是增加了?减少或增加了多少?
)中的“每日计件工资制”改为“每周计件工资制”,其他条件不变,在此方式下该厂工人一周的工资总额与“每日计件工资制”相比是减少还是增加了?减少或增加了多少?



