Question

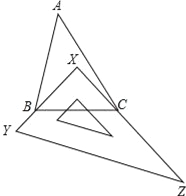
【题目】如图所示，有一块直角三角板XYZ放置在△ABC中，三角板的两条直角边XY和XZ恰好分别经过点B和点C．

（1）若∠A=30°，则∠ABX+∠ACX的大小是多少？

（2）若改变三角板的位置，但仍使点B，点C在三角板的边XY和边XZ上，此时∠ABX+∠ACX的大小有变化吗？请说明你的理由．

Answer 1

【答案】（1）60°；（2）∠ABX+∠ACX的大小没有变化；理由见解析.

【解析】试题分析：（1）在△ABC中，利用三角形内角和得出∠ABC+∠ACB=180°﹣∠A，即可求∠ABC+∠ACB；同理在△XBC中，∠BXC=90°，那么∠XBC+∠XCB=90°，即可得出结果；

（2）在△ABC中，∠ABC+∠ACB=180°﹣∠A是一个定值，同理在△XBC中，∠BXC=90°，∠XBC+∠XCB=90°也是一个定值，∠ABX+∠ACX=90°﹣∠A的值不变．

试题解析：（1）∵∠A=30°，

∴∠ABC+∠ACB=180°﹣∠A=180°﹣30°=150°，

∵∠YXZ=90°，

∴∠XBC+∠XCB=90°，

∴∠ABX+∠ACX=150°﹣90°=60°；

（2）∠ABX+∠ACX的大小没有变化.理由如下：

∵∠ABC+∠ACB=180°﹣∠A，∠YXZ=90°，

∴∠XBC+∠XCB=90°，

∴∠ABX+∠ACX=180°﹣∠A﹣90°=90°﹣∠A；

即∠ABX+∠ACX的大小没有变化．