题目内容
如图,在直角坐标系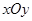 中,Rt△OAB和Rt△OCD的直角顶点A,C始终在
中,Rt△OAB和Rt△OCD的直角顶点A,C始终在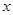 轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,Rt△OAB的面积恒为
轴的正半轴上,B,D在第一象限内,点B在直线OD上方,OC=CD,OD=2,M为OD的中点,AB与OD相交于E,当点B位置变化时,Rt△OAB的面积恒为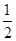 .试解决下列问题:
.试解决下列问题:
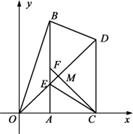
(1)填空:点D坐标为 ;
(2)设点B横坐标为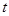 ,请把BD长表示成关于
,请把BD长表示成关于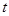 的函数关系式,并化简;
的函数关系式,并化简;
(3)等式BO=BD能否成立?为什么?
(4)设CM的延长线与AB相交于F,当△BDE为直角三角形时,判断四边形BDCF的形状(无需证明).
(1)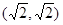 ;
;
(2)
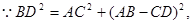
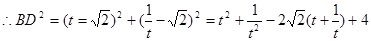 ①
①
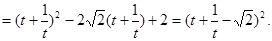
 ②
②
(3)若OB=BD,则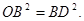
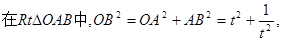
由①得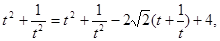
得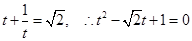
∴△ ,∴此方程无解
,∴此方程无解
∴OB≠BD
(4)如果△BDE为直角三角形,
①当∠EBD=90º时,此时四边形BDCF为直角梯形.
②当∠EDB=90º时,此时四边形BDCF为菱形
【解析】(1)在Rt△OCD中,根据勾股定理易求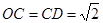 ;
;
(2)根据Rt△OAB的面积是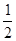 可求出B点的坐标,因为
可求出B点的坐标,因为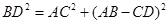 ,所以把B点的坐标代入可得BD长,即可表示成关于t的函数关系式.
,所以把B点的坐标代入可得BD长,即可表示成关于t的函数关系式.
(3)假设OB=BD,在Rt△OAB中,用t把OB表示出来,根据题(2)中用t表示的BD.两者相等,可得一二次函数表达式,用根的判别式判断是否有解.
(4)两种情况,先假设∠EBD=90°时(如图2),此时F、E、M三点重合,根据已知条件此时四边形BDCF为直角梯形,然后假设∠EDB=90°时(如图3),根据已知条件,此时四边形BDCF为平行四边形,在Rt△OCD中,OB2=OD2+BD2,用t把各线段表示出来代入,可求出 ,即此时四边形BDCF为菱形.
,即此时四边形BDCF为菱形.

 名校课堂系列答案
名校课堂系列答案
 如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.
如图,在直角坐标系中,点P的坐标为(3,4),将OP绕原点O逆时针旋转90°得到线段OP′.

 ,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件:
,2).画出△ABC的两个位似图形△A1B1C1,△A2B2C2,同时满足下列两个条件: