题目内容
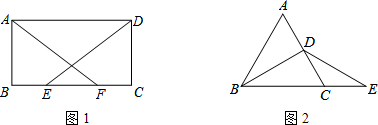
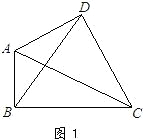
 如图,E为矩形ABCD的边CD上的一点,AB=AE=4,BC=2,则∠BEC是
如图,E为矩形ABCD的边CD上的一点,AB=AE=4,BC=2,则∠BEC是
- A.15度
- B.30度
- C.60度
- D.75度
D
分析:先根据直角三角形的性质求出∠1的度数,再根据平行线的性质求出∠3的度数,由AB=AE求出∠4度数,再由平角的性质解答即可.
解答: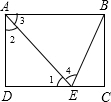 解:∵在Rt△ADE中,AD=2,AE=4,
解:∵在Rt△ADE中,AD=2,AE=4,
∴∠1=30°,
∵AB∥CD,∴∠3=∠1=30°,
∵AB=AE,∴∠4= =
= =75°,
=75°,
∴∠BEC=180°-∠1-∠4=180°-30°-75°=75°.
点评:本题考查的是矩形、直角三角形及等腰三角形的性质,比较简单.
分析:先根据直角三角形的性质求出∠1的度数,再根据平行线的性质求出∠3的度数,由AB=AE求出∠4度数,再由平角的性质解答即可.
解答:
 解:∵在Rt△ADE中,AD=2,AE=4,
解:∵在Rt△ADE中,AD=2,AE=4,∴∠1=30°,
∵AB∥CD,∴∠3=∠1=30°,
∵AB=AE,∴∠4=
 =
= =75°,
=75°,∴∠BEC=180°-∠1-∠4=180°-30°-75°=75°.
点评:本题考查的是矩形、直角三角形及等腰三角形的性质,比较简单.

练习册系列答案
相关题目
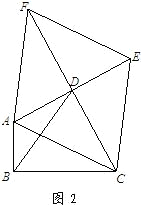
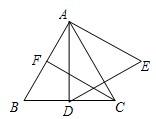 26、如图,在等边△ABC中,点D是BC边的中点,以AD为边作等边△ADE.
26、如图,在等边△ABC中,点D是BC边的中点,以AD为边作等边△ADE.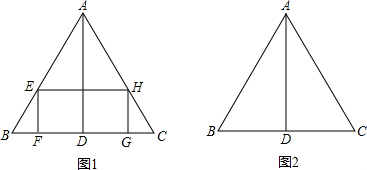
 如图,四边形DEFG是△ABC的内接矩形,如果△ABC的高线AH长8cm,底边BC长10cm,设DG=xcm,DE=ycm,则y关于x的函数关系式为
如图,四边形DEFG是△ABC的内接矩形,如果△ABC的高线AH长8cm,底边BC长10cm,设DG=xcm,DE=ycm,则y关于x的函数关系式为