题目内容
已知反比例函数 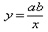 ,当
,当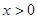 时,
时, 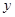 随
随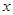 的增大而增大,则关
的增大而增大,则关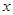 于的方程
于的方程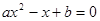 的解的情是 .
的解的情是 .
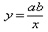 ,当
,当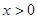 时,
时, 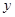 随
随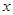 的增大而增大,则关
的增大而增大,则关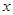 于的方程
于的方程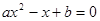 的解的情是 .
的解的情是 .有两个不相等的实数根
根据反比例函数y=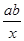 的性质可以得到ab<0;然后计算关于x的方程ax2-2x+b=0的根的判别式△=4-4ab=4(1-ab)的符号,根据根的判别式的符号确定该方程的根的情况.
的性质可以得到ab<0;然后计算关于x的方程ax2-2x+b=0的根的判别式△=4-4ab=4(1-ab)的符号,根据根的判别式的符号确定该方程的根的情况.
解:∵反比例函数y=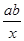 ,当x>0时,随x的增大而增大,
,当x>0时,随x的增大而增大,
∴ab<0;
∴-ab>0,
∴1-ab>1;
∴关于x的方程ax2-2x+b=0的根的判别式△=4-4ab=4(1-ab)>4>0,
∴该方程有两个不相等的实数根.
故答案是:②.
本题主要考查了一元二次方程的根的判别式与反比例函数的性质.根据反比例函数的性质求得ab<0是解题的关键.
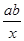 的性质可以得到ab<0;然后计算关于x的方程ax2-2x+b=0的根的判别式△=4-4ab=4(1-ab)的符号,根据根的判别式的符号确定该方程的根的情况.
的性质可以得到ab<0;然后计算关于x的方程ax2-2x+b=0的根的判别式△=4-4ab=4(1-ab)的符号,根据根的判别式的符号确定该方程的根的情况.解:∵反比例函数y=
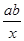 ,当x>0时,随x的增大而增大,
,当x>0时,随x的增大而增大,∴ab<0;
∴-ab>0,
∴1-ab>1;
∴关于x的方程ax2-2x+b=0的根的判别式△=4-4ab=4(1-ab)>4>0,
∴该方程有两个不相等的实数根.
故答案是:②.
本题主要考查了一元二次方程的根的判别式与反比例函数的性质.根据反比例函数的性质求得ab<0是解题的关键.

练习册系列答案
相关题目
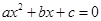 的根为2和3,则关于x的一元二次方程
的根为2和3,则关于x的一元二次方程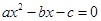 的根为( ).
的根为( ).

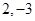

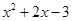



 有两个同号的实数根,m的取值范围是 ( )
有两个同号的实数根,m的取值范围是 ( )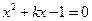 ,是否存在实数k,使得方程有两根分别为
,是否存在实数k,使得方程有两根分别为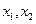 且满足
且满足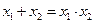 ,若有求出k的值;若没有,请说明理由。
,若有求出k的值;若没有,请说明理由。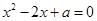 有两个相等的实数根,那么a=________.
有两个相等的实数根,那么a=________.