��Ŀ����
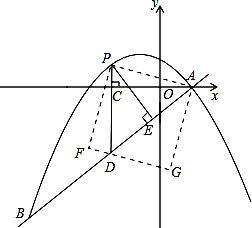
����Ŀ����ͼ������ABC�У�BC��5����AD��BE�ཻ�ڵ�O��BD��![]() CD����AE��BE��
CD����AE��BE��
��1�����߶�AO�ij���
��2������P�ӵ�O���������߶�OA��ÿ��1����λ���ȵ��ٶ����յ�A�˶�������Q�ӵ�B����������BC��ÿ��4����λ���ȵ��ٶ��˶���P��Q����ͬʱ����������P����A��ʱ��P��Q����ͬʱֹͣ�˶������P���˶�ʱ��Ϊt�룬��POQ�����ΪS�����ú�t��ʽ�ӱ�ʾS����ֱ��д����Ӧ��t��ȡֵ��Χ��
��3���ڣ�2���������£���F��ֱ��AC�ϵ�һ����CF��BO���Ƿ����tֵ��ʹ�Ե�B��O��PΪ��������������Ե�F��C��QΪ�����������ȫ�ȣ������ڣ���ֱ��д������������tֵ���������ڣ���˵�����ɣ�
���𰸡���1��AO��BC��5����2����S����2t2+t��0��t��![]() ������S��2t2��t��
������S��2t2��t��![]() ��t��5������3�����ڣ�t��1��
��t��5������3�����ڣ�t��1��![]() s��
s��
��������
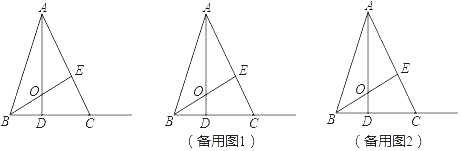
��1��ֻҪ֤����AOE�ա�BCE���ɽ�����⣻
��2������������������⼴�ɢٵ���Q���߶�BD��ʱ��QD��2��4t���ڵ���Q������DC��ʱ��DQ��4t��2ʱ��
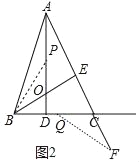
��3��������������⼴�ɢ���ͼ2�У���OP��CQʱ��BOP�ա�FCQ������ͼ3�У���OP��CQʱ����BOP�ա�FCQ.
�⣺��1����ͼ1�У�
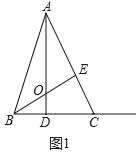
��AD�Ǹߣ�
���ADC��90����
��BE�Ǹߣ�
���AEB����BEC��90����
���EAO+��ACD��90������EBC+��ECB��90����
���EAO����EBC��
����AOE����BCE��
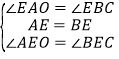 ��
��
���AOE�ա�BCE��
��AO��BC��5��
��2����BD��![]() CD��BC��5��
CD��BC��5��
��BD��2��CD��3��
������OP��t��BQ��4t��
�ٵ���Q���߶�BD��ʱ��QD��2��4t��
��S��![]() t��2��4t������2t2+t��0��t��
t��2��4t������2t2+t��0��t��![]() ����
����
�ڵ���Q������DC��ʱ��DQ��4t��2��
��S��![]() t��4t��2����2t2��t��
t��4t��2����2t2��t��![]() ��t��5����
��t��5����
��3�����ڣ�
����ͼ2�У���OP��CQʱ����OB��CF����POB����FCQ�����BOP�ա�FCQ��
��CQ��OP��
��5��4t�Tt��
���t��1��
����ͼ3�У���OP��CQʱ����OB��CF����POB����FCQ��
���BOP�ա�FCQ��

��CQ��OP��
��4t��5��t��
���t��![]() ��
��
����������t��1��![]() sʱ����BOP����FCQȫ�ȣ�
sʱ����BOP����FCQȫ�ȣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�