题目内容
【题目】如图,海中有一灯塔P,它的周围8海里内有暗礁.海轮以18海里/时的速度由西向东航行,在A处测得灯塔P在北偏东60°方向上;航行40分钟到达B处,测得灯塔P在北偏东30°方向上;如果海轮不改变航线继续向东航行,有没有触礁的危险?
【答案】解:过P作PD⊥AB. 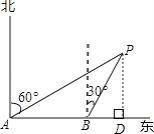
AB=18× ![]() =12海里.
=12海里.
∵∠PAB=30°,∠PBD=60°
∴∠PAB=∠APB
∴AB=BP=12海里.
在Rt△PBD中,PD=BPsin∠PBD=12× ![]() =6
=6 ![]() 海里.
海里.
∵6 ![]() >8
>8
∴海轮不改变方向继续前进没有触礁的危险.
【解析】过P作PD⊥AB.根据题意求出AB的长,再证明∠PAB=∠APB,得到AB=BP,然后在Rt△PBD中,利用解直角三角形求出PD的长,再与8比较大小即可得出结论。
【考点精析】认真审题,首先需要了解解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法)),还要掌握关于方向角问题(指北或指南方向线与目标方向 线所成的小于90°的水平角,叫做方向角)的相关知识才是答题的关键.

练习册系列答案
相关题目