题目内容
(2002•大连)如图,在⊙O中,AB为⊙O的弦,C、D是直线AB上两点,且AC=BD,求证:△OCD为等腰三角形.
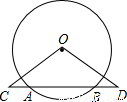
【答案】分析:此题解法较多,下面以拣两种常用的解法进行说明:
①连接OA、OB,由于OA、OB都是⊙O的半径,则OA=OB,且∠OAC=∠OBD,进而可得∠OAC=∠OBD,然后通过证△OAC≌△OBD得到OC=OD,即△OCD是等腰三角形的结论.
②过O作AB垂线,设垂足为M,由垂径定理可得AM=BM,已知AC=BD,那么CM=DM,即OM垂直平分线段CD,由此证得OC=OD,即△OCD为等腰三角形.
解答: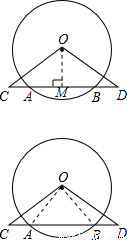 证明:(证法一)过点O点作OM⊥AB,垂足为M;
证明:(证法一)过点O点作OM⊥AB,垂足为M;
∵OM⊥AB,∴AM=BM,
∵AC=BD,∴CM=DM,
又∵OM⊥AB,∴OC=OD,
∴△OCD为等腰三角形.
(证法二)连接OA,OB;
∵OA=OB,∴∠OAB=∠OBA,
∴△CBO≌△DAO,
∴OC=OD,
∴△OCD为等腰三角形;
(证法三)(以上同证法二)
∴∠CAO=∠DBO,
又∵AC=BD,
∴△CAO≌△DBO,
∴△OCD为等腰三角形.
点评:此题主要考查了垂径定理、全等三角形的判定和性质以及等腰三角形的判定等知识,难度不大.
①连接OA、OB,由于OA、OB都是⊙O的半径,则OA=OB,且∠OAC=∠OBD,进而可得∠OAC=∠OBD,然后通过证△OAC≌△OBD得到OC=OD,即△OCD是等腰三角形的结论.
②过O作AB垂线,设垂足为M,由垂径定理可得AM=BM,已知AC=BD,那么CM=DM,即OM垂直平分线段CD,由此证得OC=OD,即△OCD为等腰三角形.
解答:
 证明:(证法一)过点O点作OM⊥AB,垂足为M;
证明:(证法一)过点O点作OM⊥AB,垂足为M;∵OM⊥AB,∴AM=BM,
∵AC=BD,∴CM=DM,
又∵OM⊥AB,∴OC=OD,
∴△OCD为等腰三角形.
(证法二)连接OA,OB;
∵OA=OB,∴∠OAB=∠OBA,
∴△CBO≌△DAO,
∴OC=OD,
∴△OCD为等腰三角形;
(证法三)(以上同证法二)
∴∠CAO=∠DBO,
又∵AC=BD,
∴△CAO≌△DBO,
∴△OCD为等腰三角形.
点评:此题主要考查了垂径定理、全等三角形的判定和性质以及等腰三角形的判定等知识,难度不大.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 =
=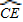 ,
, ,tan∠ECB=
,tan∠ECB= ,求经过A、B、C三点的抛物线的解析式;
,求经过A、B、C三点的抛物线的解析式; AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.
AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.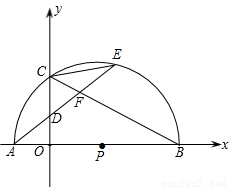
 =
=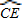 ,
, ,tan∠ECB=
,tan∠ECB= ,求经过A、B、C三点的抛物线的解析式;
,求经过A、B、C三点的抛物线的解析式; AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.
AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.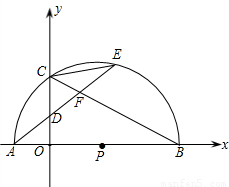
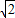 ,则⊙O1的半径为 .
,则⊙O1的半径为 .