题目内容
(2002•大连)如图,P为x轴正半轴上一点,半圆P交x轴于A、B两点,交y轴于C点,弦AE分别交OC、CB于D、F.已知
 =
=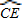 ,
,(1)求证:AD=CD;
(2)若DF=
 ,tan∠ECB=
,tan∠ECB= ,求经过A、B、C三点的抛物线的解析式;
,求经过A、B、C三点的抛物线的解析式;(3)设M为x轴负半轴上一点,OM=
 AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.
AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.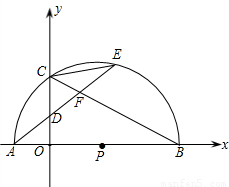
【答案】分析:(1)连接AC,根据圆周角定理知∠ACB=90°,已知OC⊥AB,易证得∠ACO=∠OBC,因此只需证得∠DAC=∠ABC;由于C是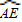 的中点,那么∠CAE=∠CBA,由此可得∠ACD=∠CAD,即可得证.
的中点,那么∠CAE=∠CBA,由此可得∠ACD=∠CAD,即可得证.
(2)在Rt△ACB和Rt△ACF中,∠DCF和∠DFC是等角的余角,因此两角相等,由此可得CD=DF=AD,即可得到AD的长,已知了∠ECO即∠DAO得正切值,可用未知数表示出OA、OD的长,进而由勾股定理求出OA、OD的长,也就能求出OC的长;由相交弦定理得:OC2=OA•OB,即可求出OB的长,从而得到A、B、C三点的坐标,利用待定系数法即可求出该抛物线的解析式.
(3)由(2)可求得⊙P的直径,根据∠EAB的余弦值即可求出AE的长,从而求出OM的值,也就得到了M点的坐标.设出过点M的直线解析式,将点M的坐标代入其中,即可消去一个待定系数,联立抛物线的解析式,消去y后可得关于x的一元二次方程,由于两个函数的交点到y轴的距离相等,因此它们的横坐标互为相反数,利用根与系数的关系即可确定该直线解析式中的待定系数,然后再判断此时的方程是否有实数根即可,若有实数根,则存在符合条件的直线,反之则不存在.
解答: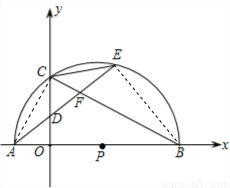 (1)证明:连接AC,
(1)证明:连接AC,
∵AB为半圆P的直径,
∴∠ACB=90°,
∴∠ACO+∠BCO=90°,
又∵OC⊥AB,
∴∠COB=90°,
∴∠ABC+∠BCO=90°,
∴∠ACO=∠ABC,
∵ ,
,
∴∠ABC=∠CAE,
∴∠ACO=∠CAE,
∴AD=CD.
(2)解:∵∠ACB=90°,
∴∠CAE+∠CFA=90°,∠ACO+∠BCO=∠90°,
∴∠BCO=∠CFA,
∴CD=DF,
∴AD=CD=DF= ,
,
∴OD=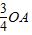 ;
;
由勾股定理得OA2+OD2=AD2
∴OA2+( AO)2=(
AO)2=( )2
)2
∴OA=1,OD= ,
,
∴OC=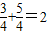 ,
,
由相交弦定理得OC2=4,
∴A点坐标为(-1,0),B点坐标为(4,0),C点坐标为(0,2),
设过A,B,C三点的抛物线解析式为y=a(x+1)(x-4),
∴a=- ,
,
∴y=- (x+1)(x-4)=-
(x+1)(x-4)=- x2+
x2+ x+2.
x+2.
(3)解:不存在;
理由,假设存在过点M的直线符合题目的条件,连接EB,
∵AB=1+4=5,又AB为半圆直径,
∴∠AEB=90°,
∴EB=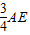 ,
,
∴AE=4,
∴OM=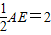 ,
,
∵M点在x轴负半轴上,
∴M点的坐标为(-2,0);
设过M点的直线解析式为y=kx+b,则-2k+b=0,
∴b=2k,
∴y=kx+2k,
由题意,方程组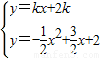 有两个解,消去y,
有两个解,消去y,
得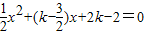 ①,
①,
方程①应有两个不等式的实数根,
∵所求直线与抛物线的两个交点到y轴距离相等,
∴方程①两根互为相反数,即两根之和为0;
∴k= ,
,
∴原方程无实数解;
∴满足题目条件的直线不存在.
点评:此题考查的知识点有:圆周角定理、等腰三角形的性质、解直角三角形、相交弦定理、二次函数解析式的确定、函数图象交点坐标的求法以及根与系数的关系、根的判别式等知识,涉及的知识范围较广,综合性强,难度较大.
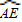 的中点,那么∠CAE=∠CBA,由此可得∠ACD=∠CAD,即可得证.
的中点,那么∠CAE=∠CBA,由此可得∠ACD=∠CAD,即可得证.(2)在Rt△ACB和Rt△ACF中,∠DCF和∠DFC是等角的余角,因此两角相等,由此可得CD=DF=AD,即可得到AD的长,已知了∠ECO即∠DAO得正切值,可用未知数表示出OA、OD的长,进而由勾股定理求出OA、OD的长,也就能求出OC的长;由相交弦定理得:OC2=OA•OB,即可求出OB的长,从而得到A、B、C三点的坐标,利用待定系数法即可求出该抛物线的解析式.
(3)由(2)可求得⊙P的直径,根据∠EAB的余弦值即可求出AE的长,从而求出OM的值,也就得到了M点的坐标.设出过点M的直线解析式,将点M的坐标代入其中,即可消去一个待定系数,联立抛物线的解析式,消去y后可得关于x的一元二次方程,由于两个函数的交点到y轴的距离相等,因此它们的横坐标互为相反数,利用根与系数的关系即可确定该直线解析式中的待定系数,然后再判断此时的方程是否有实数根即可,若有实数根,则存在符合条件的直线,反之则不存在.
解答:
 (1)证明:连接AC,
(1)证明:连接AC,∵AB为半圆P的直径,
∴∠ACB=90°,
∴∠ACO+∠BCO=90°,
又∵OC⊥AB,
∴∠COB=90°,
∴∠ABC+∠BCO=90°,
∴∠ACO=∠ABC,
∵
 ,
,∴∠ABC=∠CAE,
∴∠ACO=∠CAE,
∴AD=CD.
(2)解:∵∠ACB=90°,
∴∠CAE+∠CFA=90°,∠ACO+∠BCO=∠90°,
∴∠BCO=∠CFA,
∴CD=DF,
∴AD=CD=DF=
 ,
,∴OD=
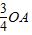 ;
;由勾股定理得OA2+OD2=AD2
∴OA2+(
 AO)2=(
AO)2=( )2
)2∴OA=1,OD=
 ,
,∴OC=
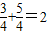 ,
,由相交弦定理得OC2=4,
∴A点坐标为(-1,0),B点坐标为(4,0),C点坐标为(0,2),
设过A,B,C三点的抛物线解析式为y=a(x+1)(x-4),
∴a=-
 ,
,∴y=-
 (x+1)(x-4)=-
(x+1)(x-4)=- x2+
x2+ x+2.
x+2.(3)解:不存在;
理由,假设存在过点M的直线符合题目的条件,连接EB,
∵AB=1+4=5,又AB为半圆直径,
∴∠AEB=90°,
∴EB=
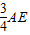 ,
,∴AE=4,
∴OM=
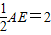 ,
,∵M点在x轴负半轴上,
∴M点的坐标为(-2,0);
设过M点的直线解析式为y=kx+b,则-2k+b=0,
∴b=2k,
∴y=kx+2k,
由题意,方程组
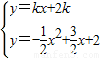 有两个解,消去y,
有两个解,消去y,得
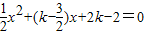 ①,
①,方程①应有两个不等式的实数根,
∵所求直线与抛物线的两个交点到y轴距离相等,
∴方程①两根互为相反数,即两根之和为0;
∴k=
 ,
,∴原方程无实数解;
∴满足题目条件的直线不存在.
点评:此题考查的知识点有:圆周角定理、等腰三角形的性质、解直角三角形、相交弦定理、二次函数解析式的确定、函数图象交点坐标的求法以及根与系数的关系、根的判别式等知识,涉及的知识范围较广,综合性强,难度较大.

练习册系列答案
相关题目
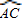 =
=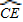 ,
, ,tan∠ECB=
,tan∠ECB= ,求经过A、B、C三点的抛物线的解析式;
,求经过A、B、C三点的抛物线的解析式; AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.
AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.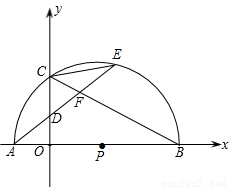
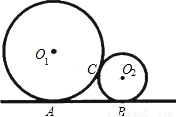
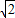 ,则⊙O1的半径为 .
,则⊙O1的半径为 .