题目内容
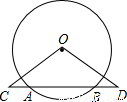
(2002•大连)如图,BC为⊙O的直径,弦BD和弦EC的延长线相交于点A,△ADE和△ABC的面积之比为3:4,则∠BAC的度数为 °,若BC=2,则弓形DCE的面积为 平方单位.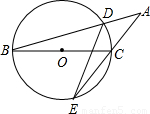
【答案】分析:连接CD、BE.根据直径所对的圆周角为90°,及相似三角形的判定和性质,相似三角形的面积比是相似比的平方得出∠BAC的度数.再根据同弧所对的圆心角和圆周角的关系得出∠DOE=120°,由弓形DCE的面积=S扇形ODE-S△ODE得出结果.
解答: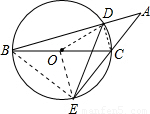 解:连接CD、BE.
解:连接CD、BE.
∵∠A=∠A,∠ABC=∠AED,BC为⊙O的直径,
∴∠BDC=∠ADC=∠AEB=90°,
∴△ABC∽△AED,△ABE∽△ACD.
∵△ADE和△ABC的面积之比为3:4,
∴AE:AB=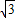 :2,
:2,
∴∠BAC=30°,∠ABE=60°.
连接OD、OE.
∵∠ABE=60°,
∴∠DOE=120°,
∴弓形DCE的面积=S扇形ODE-S△ODE
=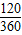 ×π•22-
×π•22- ×(2÷2×
×(2÷2×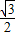 ×2)×(2÷2×
×2)×(2÷2× )
)
=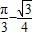 平方单位.
平方单位.
点评:本题考查了相似三角形的判定和性质,圆的有关性质.另外不规则图形的面积一定要注意分割成规则图形的面积进行计算.
解答:
 解:连接CD、BE.
解:连接CD、BE.∵∠A=∠A,∠ABC=∠AED,BC为⊙O的直径,
∴∠BDC=∠ADC=∠AEB=90°,
∴△ABC∽△AED,△ABE∽△ACD.
∵△ADE和△ABC的面积之比为3:4,
∴AE:AB=
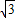 :2,
:2,∴∠BAC=30°,∠ABE=60°.
连接OD、OE.
∵∠ABE=60°,
∴∠DOE=120°,
∴弓形DCE的面积=S扇形ODE-S△ODE
=
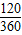 ×π•22-
×π•22- ×(2÷2×
×(2÷2×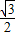 ×2)×(2÷2×
×2)×(2÷2× )
)=
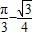 平方单位.
平方单位.点评:本题考查了相似三角形的判定和性质,圆的有关性质.另外不规则图形的面积一定要注意分割成规则图形的面积进行计算.

练习册系列答案
相关题目
 =
=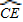 ,
, ,tan∠ECB=
,tan∠ECB= ,求经过A、B、C三点的抛物线的解析式;
,求经过A、B、C三点的抛物线的解析式; AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.
AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.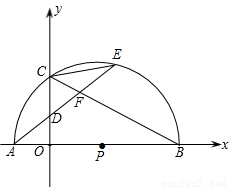
 =
=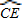 ,
, ,tan∠ECB=
,tan∠ECB= ,求经过A、B、C三点的抛物线的解析式;
,求经过A、B、C三点的抛物线的解析式; AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.
AE,是否存在过点M的直线,使该直线与(2)中所得的抛物线的两个交点到y轴距离相等?若存在,求出这条直线的解析式;若不存在,请说明理由.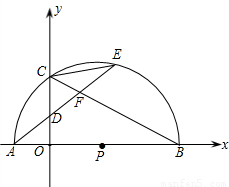
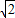 ,则⊙O1的半径为 .
,则⊙O1的半径为 .