题目内容
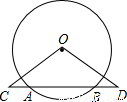
（2002•大连）如图，⊙O1和⊙O2外切于点C，直线AB分别切⊙O1和⊙O2于AB，⊙O2的半径为1，AB=2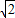
，则⊙O1的半径为 ．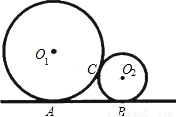
【答案】分析：连接O1O2、O1A、O2B，过O2作O1A的垂线设垂足为D，在构造的直角三角形中，易知O2D=AB，O1O2为两圆的半径和，O1D是两圆的半径差，利用勾股定理即可求得⊙O1的半径．
解答：
解：连接O1O2、O1A、O2B，过O2作O2D⊥O1A于D；
设⊙O1的半径为R，则：
O1O2=R+1，O1D=R-1，O2D=AB=2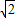
；
在Rt△O1O2D中，由勾股定理得：
（R+1）2=（R-1）2+8，
解得R=2，故⊙O1的半径为2．
点评：此题主要考查了相切两圆的性质以及勾股定理的综合应用，正确地构造出与所求相关的直角三角形是解题的关键．
解答：
解：连接O1O2、O1A、O2B，过O2作O2D⊥O1A于D；设⊙O1的半径为R，则：
O1O2=R+1，O1D=R-1，O2D=AB=2
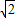；在Rt△O1O2D中，由勾股定理得：
（R+1）2=（R-1）2+8，
解得R=2，故⊙O1的半径为2．
点评：此题主要考查了相切两圆的性质以及勾股定理的综合应用，正确地构造出与所求相关的直角三角形是解题的关键．
练习册系列答案
相关题目
=
，
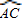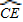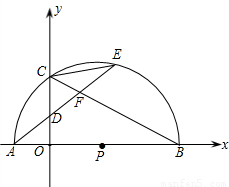
，tan∠ECB=
，求经过A、B、C三点的抛物线的解析式；
AE，是否存在过点M的直线，使该直线与（2）中所得的抛物线的两个交点到y轴距离相等？若存在，求出这条直线的解析式；若不存在，请说明理由．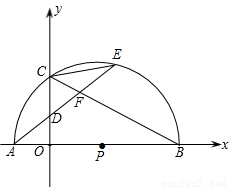
=
，
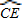，tan∠ECB=
，求经过A、B、C三点的抛物线的解析式；
AE，是否存在过点M的直线，使该直线与（2）中所得的抛物线的两个交点到y轴距离相等？若存在，求出这条直线的解析式；若不存在，请说明理由．
