Question

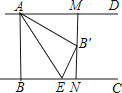
【题目】如图，在Rt△ABC中，∠ACB=90°，AC=5，BC=12，将△ABC绕点B顺时针旋转60°，得到△BDE，连接DC交AB于点F，则△ACF与△BDF的周长之和为 ___________

Answer 1

【答案】42

【解析】

根据将△ABC绕点B顺时针旋转60°，得到△BDE，可得△ABC≌△BDE，∠CBD=60°，BD=BC=12cm，从而得到△BCD为等边三角形，得到CD=BC=CD=12cm．在Rt△ACB中，利用勾股定理得到AB=13，所以△ACF与△BDF的周长之和=AC+AF+CF+BF+DF+BD=AC+AB+CD+BD，即可解答．

∵将△ABC绕点B顺时针旋转60°，得到△BDE，∴△ABC≌△BDE，∠CBD=60°，∴BD=BC=12cm，∴△BCD为等边三角形，∴CD=BC=CD=12cm．在Rt△ACB中，AB==13，△ACF与△BDF的周长之和=AC+AF+CF+BF+DF+BD=AC+AB+CD+BD=5+13+12+12=42（cm）．

故答案为：42．