题目内容
【题目】如图1,抛物线![]() ,其中
,其中![]() ,点A(-2,m)在该抛物线上,过点A作直线l∥x轴,与抛物线交于另一点B,与y轴交于点C.
,点A(-2,m)在该抛物线上,过点A作直线l∥x轴,与抛物线交于另一点B,与y轴交于点C.
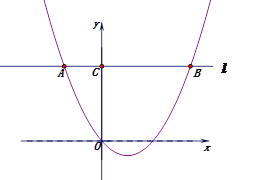
(1)求m的值.
(2)当a=2时,求点B的坐标.
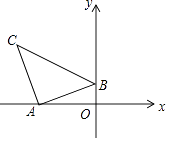
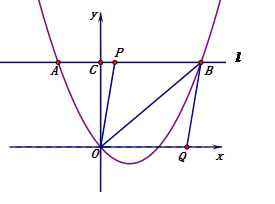
(3)如图2,以OB为对角线作菱形OPBQ,顶点P在直线l上,顶点Q在x轴上.
①若PB=2AP,求a的值.
②菱形OPBQ的面积的最小值是 .
【答案】(1)当x=-2时,y=4a-4(a-1)=4(2)点B的坐标为(1,4)(3)①![]() ②菱形的最小面积=16
②菱形的最小面积=16
【解析】(1)把x=-2代入抛物线![]() 即可得到y的值;(2)先求出抛物线表达式,然后求出x的解;(3)利用抛物线的对称轴即可求出点B的坐标和a的值以及菱形OPBQ的面积的最小值.
即可得到y的值;(2)先求出抛物线表达式,然后求出x的解;(3)利用抛物线的对称轴即可求出点B的坐标和a的值以及菱形OPBQ的面积的最小值.
解:(1)当x=-2时,![]()
(2)当a=2时,抛物线表达式为![]()
当y=4时,![]() ,
,
解得![]()
把-2舍去,点B的坐标为(1,4)
(3)①当点P在线段AB上时,设CP=x,则AP=2+x,BP=OP=4+2x
在Rt△OCP中,![]() ,
,
解得![]()
∴CP=0,CB=PB=4,点B的坐标是(4,4)
由题可知抛物线的对称轴:直线![]()
又由点A与点B关于对称轴对称,则![]() ,解得
,解得![]()
当点P在射线BA上时,设CP=x,则AP=x-2,BP=OP=2x-4
在Rt△OCP中, ![]() ,解得
,解得![]() (舍去),
(舍去),![]() ,
,
∴CP=![]() ,PB=
,PB=![]() ,CB=
,CB=![]() 点B的坐标是(
点B的坐标是(![]() ,4)
,4)
由点A与点B关于对称轴对称,则 ,解得
,解得![]()
②菱形的最小面积=16
“点睛”本题考查待定系数法确定二次函数解析式、二次函数性质等知识,解题的关键是由点A与点B关于对称轴对称求出a的值,会运用方程的思想解决问题,属于中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目