��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ����Rt��ABC����BAC=90�㣬AB=AC��A����3��0����B��0��1����C��m��n����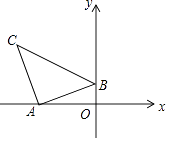
��1����ֱ��д��C�����꣮
��2������ABC��x���������ƽ��t����λ��B�䡢C������Ķ�Ӧ�㡢�������ڷ���������y= ![]() �ڵ�һ������ͼ���ϣ������t��k��ֵ��
�ڵ�һ������ͼ���ϣ������t��k��ֵ��
��3���ڣ�2���������£����Ƿ��x���ϵĵ�M�ͷ���������y= ![]() ͼ���ϵĵ�N��ʹ����B�䡢C�䣬M��NΪ������ı��ι���ƽ���ı��Σ�������ڣ�������������������ĵ�M�͵�N�����ꣻ��������ڣ���˵�����ɣ�
ͼ���ϵĵ�N��ʹ����B�䡢C�䣬M��NΪ������ı��ι���ƽ���ı��Σ�������ڣ�������������������ĵ�M�͵�N�����ꣻ��������ڣ���˵�����ɣ�
���𰸡�
��1��
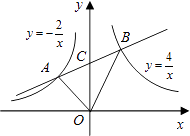
�⣺��ͼ1������C��CD��x���ڵ�D�����ADC=��AOB=90�㣬
���DAC+��ACD=90�㣬
��Rt��ABC����A=90�㣬
���DAC+��BAO=90�㣬
���BAO=��ACD��
�ڡ�ADC�͡�BOA�У�
 ��
��
���ADC�ա�BOA��AAS����
��AD=OB=1��CD=OA=3��
��OD=OA+AD=4��
��C������������4��3����

��2��
�⣺������ƽ����t����λ���ȣ����B�������Ϊ��t��1����C�������Ϊ��t��4��3����
��B�䡢C����������ij����������ͼ���ϣ�
��t=3��t��4����
��ã�t=6��
��B�䣨6��1����C�䣨2��3����
��k=6��
�෴���������Ľ���ʽΪ��y= ![]()
��3��
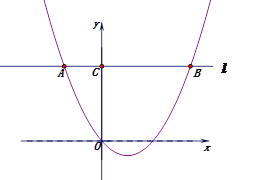
�⣺���ڣ���ͼ2��

��MNΪƽ���ı���MC��NB��ĶԽ���ʱ��
��ƽ���ı��εĶԽ�����ƽ�֣���֪B��C�䣬MN���е�Ϊͬһ���㣬
�� ![]() =
= ![]() ��
��
��yN=4����y= ![]() ��xN=1.5��
��xN=1.5��
��N��1.5��4����
�� ![]() =
= ![]() ��
��
��xM=6.5��
��M��6.5��0����
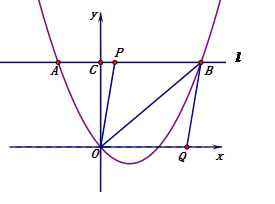
��ͼ3��

��MC��Ϊƽ���ı���MC��NB��ĶԽ���ʱ��ͬ���ɵ�M��7��0����N��3��2����
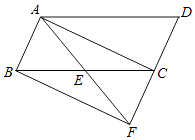
��ͼ4��

��MB��Ϊƽ���ı���MC��NB��ĶԽ���ʱ��ͬ���ɵ�M����7��0����N����3��2����
��������������M��6.5��0����N��1. 5��4����M��7��0����N��3��2����M����7��0����N����3��2����ʹ����B�䡢C�䣬M��NΪ������ı��ι���ƽ���ı��Σ�
����������1������ƽ��ֱ������ϵ����Rt��ABC����A=90�㣬AB=AC����֤�á�ADC�ա�BOA���̶����C�����ꣻ��2������������ƽ����t����λ���ȣ����B�������Ϊ��t��1����C�������Ϊ��t��4��3������B�䡢C����������ij����������ͼ���ϣ����ɵ�t=3��t��4�����̶����m��ֵ�������ø�������꣬���ǵõ����ۣ���3����ͼ2����MNΪƽ���ı���MC��NB��ĶԽ���ʱ����ͼ3����MC��Ϊƽ���ı���MC��NB��ĶԽ���ʱ����ͼ4����MB��Ϊƽ���ı���MC��NB��ĶԽ���ʱ�������е����깫ʽ���ɵõ����ۣ�
�����㾫�����������⣬������Ҫ�˽�ƽ���ı��ε��ж�(����Ա߷ֱ�ƽ�е��ı�����ƽ���ı��Σ�����Ա߷ֱ���ȵ��ı�����ƽ���ı��Σ�һ��Ա�ƽ������ȵ��ı�����ƽ���ı��Σ�����ԽǷֱ���ȵ��ı�����ƽ���ı��Σ��Խ�����ƽ�ֵ��ı�����ƽ���ı���)��

 ��ĩ���䵥Ԫ�����ิϰ��ϵ�д�
��ĩ���䵥Ԫ�����ิϰ��ϵ�д�