题目内容
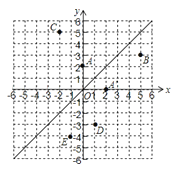
【题目】如图,在平面直角坐标系中,直线L是第一、三象限的角平分线.
(1)由图观察易知A(0,2)关于直线l的对称点A′的坐标为(2,0),请在图中分别标明B(5,3)、C(﹣2,5)关于直线l的对称点B′、C′的位置,并写出他们的坐标:B′ 、C′ ;
(2)结合图形观察以上三组点的坐标,直接写出坐标面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为 ;
(3)已知两点D(1,﹣3)、E(﹣1,﹣4),试在直线L上画出点Q,使△QDE的周长最小,并求△QDE周长的最小值.
【答案】(1)B'(3,5),C'(5,﹣2);(2)(b,a);(3)![]() 。
。
【解析】分析:(1)根据对称轴为第一、三象限的角平分线,结合图形得出B′、C′两点坐标;(2)由(1)的结论,并与B、C两点坐标进行比较,得出一般规律;(3)由轴对称性作出满足条件的Q点,求出直线D′E的解析式,与直线y=x联立,可求Q点的坐标,得出结论.
本题解析:
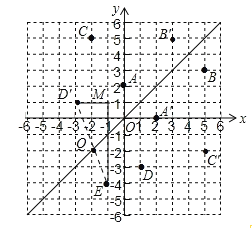
解:(1)如图,由点关于直线y=x轴对称可知:B'(3,5),C'(5,﹣2).
(2)由(1)的结果可知,坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点P′的坐标为 (b,a).
由(2)得,D(1,﹣3)关于直线l的对称点D'的坐标为(﹣3,1),连接D'E交直线l于点Q,此时点Q到D、E两点的距离之和最小,
D'E=![]() =
=![]() =
=![]() ,
,
![]() ∴
∴![]() 周长的最小值
周长的最小值![]() .+
.+![]() .
.

练习册系列答案
相关题目