题目内容
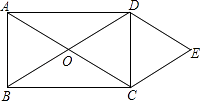
【题目】如图,AB是⊙O的直径,点C为⊙O上一点,OF⊥BC于点F,交⊙O于点E,AE与BC交于点H,点D为OE的延长线上一点,且∠ODB=∠AEC.
求证:(1)BD是⊙O的切线;(2)CE2=EH·EA.

【答案】(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由圆周角定理和已知条件证出∠ODB=∠ABC,再证出∠ABC+∠DBF=90°,即∠OBD=90°,即可得出BD是⊙O的切线;(2)连接AC,由垂径定理得出![]() ,即可得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例
,即可得出∠CAE=∠ECB,再由公共角∠CEA=∠HEC,证明△CEH∽△AEC,得出对应边成比例![]() ,即可得出结论.
,即可得出结论.
试题解析:(1)∵∠ODB=∠AEC,∠AEC=∠ABC,
∴∠ODB=∠ABC,
∵OF⊥BC,
∴∠BFD=90°,
∴∠ODB+∠DBF=90°,
∴∠ABC+∠DBF=90°,即∠OBD=90°,
∴BD⊥OB,
∴BD是⊙O的切线。
(2)连接AC,
∵OF⊥BC,
∴![]() =
=![]() ,
,
∴∠ECB=∠CAE,
又∵∠HEC=∠CEA,
∴△CEH∽△AEC,
∴![]() =
=![]() ,
,
∴CE2=EH·EA.

练习册系列答案
相关题目
【题目】为建设秀美龙江,某学校组织师生参加一年一度的植树绿化工作,准备租用7辆客车,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车x辆,租车总费用为y元,
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 60 | 40 |
租金/(元/辆) | 360 | 300 |
(1)求出y(单位:元)与x(单位:辆)之间的函数关系式。
(2)若该校共有350名师生前往参加劳动,共有多少种租车方案?
(3)带队老师从学校预支租车费用2400元,试问预支的租车费用是否可有结余?若有结余,最多可结余多少元。