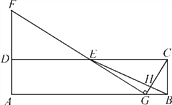
题目内容
【题目】如图,矩形ABCD的边BC与x轴重合,连接对角线BD交y轴于点E,过点A作AG⊥BD于点G,直线GF交AD于点F,AB、OC的长分别是一元二次方程x-5x+6=0的两根(AB>OC),且tan∠ADB=![]() .
.
(1)求点E、点G的坐标;
(2)直线GF分△AGD为△AGF与△DGF两个三角形,且S△AGF:S△DGF =3:1,求直线GF的解析式;
(3)点P在y轴上,在坐标平面内是否存在一点Q,使以点B、D、P、Q为顶点的四边形是矩形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.
【答案】(1)E(0, ![]() ),G(
),G(![]() ,
, ![]() );(2)
);(2)![]() ;(3)存在Q1(-4,
;(3)存在Q1(-4, ![]() );Q2(4,
);Q2(4, ![]() );Q3(0,4);Q4(0,-1).
);Q3(0,4);Q4(0,-1).
【解析】(1)根据一元二次方程x-5x+6=0的解、tan∠ADB=![]() ,可求出点E的坐标;由△BGH∽△BDC,利用相似三角形的性质可求出点G的坐标;
,可求出点E的坐标;由△BGH∽△BDC,利用相似三角形的性质可求出点G的坐标;
(2)根据G、F的坐标,利用待定系数法可求出直线GF的解析式;
(3)对BD是矩形的边还是矩形的对角线进行分类讨论即可.
解:(1)x-5x+6=0,解得x1=2;x2=3
∵AB>OC,
∴AB=3;OC=2
∵tan∠ADB=![]() ,
,
∴AD=BC=4;BD=5
∴OE=![]() ,∴E(0,
,∴E(0, ![]() )
)
∵AG⊥BD,则△ABG∽△ABD,
![]() ,即
,即![]() ,BG=
,BG=![]() ,
,
做GH⊥x轴,由△BGH∽△BDC,
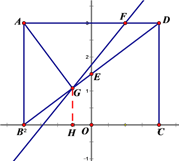
∴G(![]() ,
, ![]() )
)
(2)∵S△AGF:S△DGF =3:1,
∴AF:DF=3:1,
∴DF=1 F(1,3)
设直线GF: ![]() ,
,
代入G(![]() ,
, ![]() ),F(1,3)
),F(1,3)
∴直线GF的解析式为: ![]()
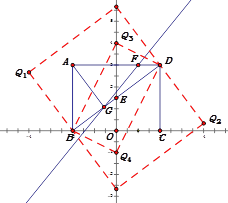
(3)存在Q1(-4, ![]() );Q2(4,
);Q2(4, ![]() );Q3(0,4);Q4(0,-1)
);Q3(0,4);Q4(0,-1)

 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案【题目】某商店一天中卖出某种品牌的运动鞋15双,它们的尺码与销售量如表所示:
鞋的尺码/cm | 23 | 23.5 | 24 | 24.5 | 25 |
销售量/双 | 2 | 3 | 3 | 5 | 2 |
则这15双鞋的尺码组成的数据中,中位数为( )
A.23.5cmB.24cmC.24.5cmD.25cm