题目内容
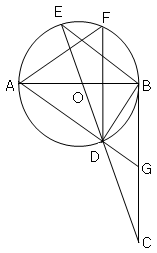
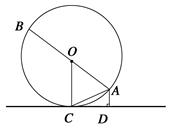
如图,已知 为⊙O的弦(非直径),
为⊙O的弦(非直径), 为
为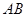 的中点,
的中点,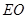 的延长线交圆于点
的延长线交圆于点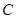 ,
,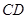 ∥
∥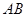 ,且交
,且交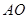 的延长线于点
的延长线于点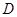 .
.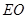 :
: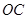
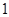 :
: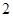 ,
,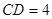 。求⊙O的半径.
。求⊙O的半径.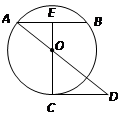
 为⊙O的弦(非直径),
为⊙O的弦(非直径),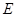 为
为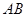 的中点,
的中点,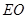 的延长线交圆于点
的延长线交圆于点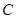 ,
,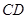 ∥
∥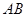 ,且交
,且交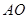 的延长线于点
的延长线于点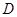 .
.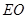 :
: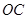
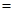
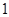 :
: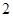 ,
,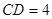 。求⊙O的半径.
。求⊙O的半径.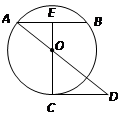

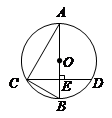
解:易证△AOE∽△DOC
∴AE:DC=OE:OC=1:2 ∵CD=4 ∴AE=2 (2分)
∵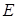 为
为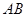 的中点 ∴OE⊥AB ∴∠AEO=
的中点 ∴OE⊥AB ∴∠AEO=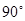
在Rt 中,根据勾股定理:
中,根据勾股定理: (4分)
(4分)
设AE= ∴OC=AO=
∴OC=AO=
则
∴ =
=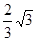 ∴AO=
∴AO=
即⊙O的半径为 (7分)
(7分)
根据E为AB的中点,则OE⊥AB,根据CD∥AB,可以得到△AEO∽△DCO,根据相似三角形的对应边的比相等,可以求出AE,在Rt△AOE中,根据勾股定理,就得到半径.
∴AE:DC=OE:OC=1:2 ∵CD=4 ∴AE=2 (2分)
∵
 为
为 的中点 ∴OE⊥AB ∴∠AEO=
的中点 ∴OE⊥AB ∴∠AEO=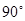
在Rt
 中,根据勾股定理:
中,根据勾股定理: (4分)
(4分)设AE=
 ∴OC=AO=
∴OC=AO=
则

∴
 =
=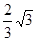 ∴AO=
∴AO=
即⊙O的半径为
 (7分)
(7分)根据E为AB的中点,则OE⊥AB,根据CD∥AB,可以得到△AEO∽△DCO,根据相似三角形的对应边的比相等,可以求出AE,在Rt△AOE中,根据勾股定理,就得到半径.

练习册系列答案
相关题目
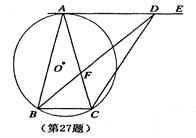
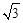 ,FC=
,FC=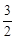 ,求AB长.
,求AB长.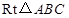 中,斜边
中,斜边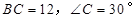 ,
,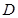 为
为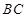 的中点,
的中点,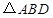 的外接圆
的外接圆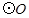 与
与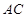 交于
交于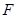 点,过
点,过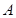 作
作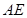 交
交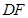 的延长线于
的延长线于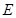 点.
点.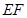 的长.
的长.

 ,则它的圆心角的度数为_____________.
,则它的圆心角的度数为_____________.