题目内容
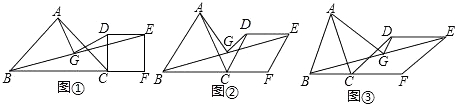
【题目】在△ABC中,AB=AC,点F是BC延长线上一点,以CF为边,作菱形CDEF,使菱形CDEF与点A在BC的同侧,连结BE,点G是BE的中点,连结AG、DG.
(1)如图①,当∠BAC=∠DCF=90°时,已知AC=3![]() ,CD=2,求AG的长度;
,CD=2,求AG的长度;
(2)如图②,当∠BAC=∠DCF=60°时,AG与DG有怎样的位置和数量关系,并证明;
(3)当∠BAC=∠DCF=α时,试探究AG与DG的位置和数量关系(数量关系用含α的式子表达).
【答案】(1)、![]() ;(2)、AG⊥GD,AG=DG;证明过程见解析;(3)、DG=AGtan
;(2)、AG⊥GD,AG=DG;证明过程见解析;(3)、DG=AGtan![]() ;证明过程见解析.
;证明过程见解析.
【解析】
试题分析:(1)、延长DG与BC交于H,先证△BG△≌EGD,得到BH=DC,=ED,HG=DG,得出BH,再证△ABH≌△ACD,得出∠BAH∠=∠CAD,AH=AD,进而求得∠HAD=90°,即可;(2)、延长DG与BC交于H,先证△BG△≌EGD,得到BH=DC,=ED,HG=DG,得出BH,再证△ABH≌△ACD,得出∠BAH∠=∠CAD,AH=AD,得到△H△AD为等边三角形,即可;(3)、延长DG与BC交于H,先证△BG△≌EGD,得到BH=DC,=ED,HG=DG,得出BH,再证△ABH≌△ACD,得出∠BAH∠=∠CAD,AH=AD,得到△H△AD为等腰三角形,即可.
试题解析:(1)、如图1,延长DG与BC交于H,连接AH、AD,
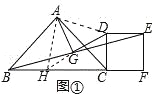
∵四边形DCEF是正方形, ∴DE=DC,DE∥CF, ∴∠GBH=∠GED,∠GHB=∠GDE, ∵G是BC的中点,
∴BG=EG, 在△BGH和△EGD中, ∵∠GBH=∠GED,∠GHB=∠GDE,BG=EG, ∴△BGH≌△EGD(AAS),
∴BH=ED,HG=DG, ∴BH=DC, ∵AB=AC,∠BAC=90°, ∴∠ABC=∠ACB=45°, ∵∠DCF=90°,
∴∠DCB=90°, ∴∠ACD=45°, ∴∠ABH=∠ACD=45°, 在△ABH和△ACD中, ∵AB=AC,∠ABH=∠ACD,BH=CD, ∴△ABH≌△ACD(SAS), ∴∠BAH=∠CAD,AH=AD, ∵∠BAH+∠HAC=90°,
∴∠CAD+∠HAC=90°, 即∠HAD=90°, ∴AG⊥GD,AG=GD; 在Rt△ABC中,AB=AC=![]() ,
,
∴BC=6 在Rt△DCH中,DC=2,HC=BC﹣BH=6﹣2=4, ∴DH=![]() =2
=2![]() , ∴GD=
, ∴GD=![]() DH=
DH=![]() ,
,
∴AG=GD=![]() .
.
(2)AG⊥GD,AG=DG;
如图2,延长DG与BC交于H,连接AH、AD,
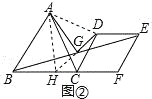
∵四边形DCEF是正方形, ∴DE=DC,DE∥CF, ∴∠GBH=∠GED,∠GHB=∠GDE, ∵G是BC的中点,
∴BG=EG,在△BGH和△EGD中, ∵∠GBH=∠GED,∠GHB=∠GDE,BG=EG, ∴△BGH≌△EGD(AAS),
∴BH=ED,HG=DG, ∴BH=DC, ∵AB=AC,∠BAC=∠DCF=60, ∴∠ABC=60°,∠ACD=60°,
∴∠ABC=∠ACD=60°, 在△ABH和△ACD中, ∵AB=AC,∠ABH=∠ACD,BH=CD, ∴△ABH≌△ACD(SAS),/p>
∴∠BAH=∠CAD,AH=AD, ∴∠BAC=∠HAD=60°, ∴AG⊥HD,∠HAG=∠DAG=30°,
∴tan∠DAG=tan30°=![]() , ∴AG=DG;
, ∴AG=DG;
(3)如图3,延长DG与BC交于H,连接AH、AD,
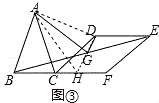
∵四边形DCEF是正方形, ∴DE=DC,DC∥CF, ∴∠GBH=∠GED,∠GHB=∠GDE, ∵G是BC中点,
∴BG=EG, ∴△BGH△≌△EGD, ∴BH=ED,HG=DG, ∴BH=DC, ∵AB=AC,∠BAC=DCF=α,
∴∠ABC=90°﹣![]() ,∠ACD=90°﹣
,∠ACD=90°﹣![]() , ∴∠ABC=ACD, ∵AB=AC,∠ABH=∠ACD,BH=CD,
, ∴∠ABC=ACD, ∵AB=AC,∠ABH=∠ACD,BH=CD,
∴△ABH≌△ACD, ∴∠BAH=∠CAD,AH=AD, ∴∠BAC=HAD=α, ∴AG⊥HD,∠HAG=∠DAG=![]() ,
,
∴tan∠DAG=tan![]() =
=![]() , ∴DG=AGtan
, ∴DG=AGtan![]() .
.

【题目】甲、乙、丙、丁四名射击选手,在相同条件下各射靶10次,他们的成绩统计如下表所示,
若要从他们中挑选一位成绩最高且波动较小的选手参加射击比赛,那么一般应选( )
甲 | 乙 | 丙 | 丁 | |
平均数(环) | 9 | 9.5 | 9 | 9.5 |
方差 | 3.5 | 4 | 4 | 5.4 |
A. 甲 B. 乙 C. 丙 D. 丁
