题目内容
如图,已知在扇形OAB中,∠AOB=90°,半径OA=10,正方形FCDE的四个顶点分别在 和半径OA、OB上,则CD的长为
.
和半径OA、OB上,则CD的长为
.

【答案】
2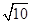 .
.
【解析】
试题分析:过点O作OH⊥CF于点H,交DE于点K,连接OF,由垂径定理可知CH=HF,因为四边形FCDE是正方形故OH⊥DE,DK=EK,所以△OEK是等腰直角三角形,OK=EK,设CD=x,则HK=x,HF=OK=EK=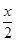 ,在Rt△OGF中根据勾股定理可得出x的值,进而得出结论.
,在Rt△OGF中根据勾股定理可得出x的值,进而得出结论.
试题解析:过点O作OH⊥CF于点H,交DE于点K,连接OF,如图:
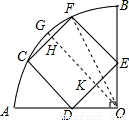
∵OH过圆心,
∴CH=HF,
∵四边形FCDE是正方形,
∴OH⊥DE,DK=EK,
∴△OEK是等腰直角三角形,OK=EK,
设CD=x,则HK=x,HF=OK=EK=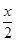 ,
,
在Rt△OGF中,OH2+HF2=OF2,即(x+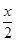 )2+(
)2+(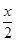 )2=102,解得x=2
)2=102,解得x=2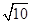 .
.
即CD的长为2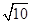 .
.
故答案为:2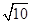 .
.
考点: 1.垂径定理;2.勾股定理;3.正方形的性质.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
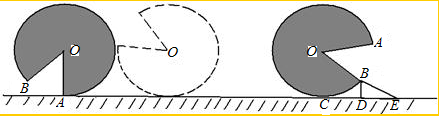



 的扇形AOB,半径OA=3cm,且OA与地面垂直.在没有滑动的情况下,将扇形向右滚动至与三角块BDE接触为止,此时,扇形与地面的接触点为C,已知∠BCD=30°,则O点移动的距离为( )
的扇形AOB,半径OA=3cm,且OA与地面垂直.在没有滑动的情况下,将扇形向右滚动至与三角块BDE接触为止,此时,扇形与地面的接触点为C,已知∠BCD=30°,则O点移动的距离为( )
