题目内容
【题目】如图,D是⊙O直径CA延长线上一点,点B在⊙O上,且AB=AD=AO.
(1)求证:BD是⊙O的切线.
(2)若E是劣弧![]() 上一点,AE与BC相交于点F,△BEF的面积为9,且cos∠BFA=
上一点,AE与BC相交于点F,△BEF的面积为9,且cos∠BFA=![]() ,求△ACF的面积.
,求△ACF的面积.

【答案】(1)证明见解析(2)16
【解析】试题分析:(1)利用斜边上的中线等于斜边的一半,可判断![]() 是直角三角形,则
是直角三角形,则![]()
![]() 是
是![]() 的切线;
的切线;
(2)同弧所对的圆周角相等,可证明![]() ,得出相似比,再利用三角形的面积比等于相似比的平方即可求解.
,得出相似比,再利用三角形的面积比等于相似比的平方即可求解.
试题解析:(1)证明:连接BO,
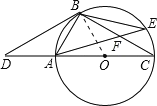
方法一:∵AB=AD,
∴∠D=∠ABD,
∵AB=AO.
∴∠ABO=∠AOB.
又在△OBD中, ![]()
![]() 即BD⊥BO.
即BD⊥BO.
∴BD是![]() 的切线;
的切线;
方法二:∵AB=AO,BO=AO.
∴AB=AO=BO.
∴△ABO为等边三角形
![]()
![]()
![]()
又![]()
![]()
![]()
即BD⊥BO,
∴BD是![]() 的切线;
的切线;
方法三:∵AB=AD=AO,
∴点O、B.D在以OD为直径的A上,
![]() 即BD⊥BO,
即BD⊥BO,
∴BD是![]() 的切线;
的切线;
(2)∵∠C=∠E,∠CAF=∠EBF,
∴△ACF∽△BEF,
∵AC是![]() 的直径.
的直径.
![]()
在Rt△BFA中, ![]()
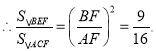
又![]()
![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】甲乙两名运动员进行射击选拨赛,每人射击10次,其中射击中靶情况如下表:
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | 第七次 | 第八次 | 第九次 | 第十次 | |
甲 | 7 | 10 | 8 | 10 | 9 | 9 | 10 | 8 | 10 | 9 |
乙 | 10 | 7 | 10 | 9 | 9 | 10 | 8 | 10 | 7 | 10 |
(1)选手甲的成绩的中位数是__________分;选手乙的成绩的众数是__________分;
(2)计算选手甲的平均成绩和方差;
(2)已知选手乙的成绩的方差是1.4,则成绩较稳定的是哪位选手?(直按写出结果)





