题目内容
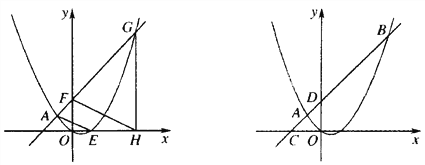
【题目】如图，直线y=kx+b分别交x轴、y轴于A（1，0）、B（0，﹣1），交双曲线y=
于点C、D．
（1）求k、b的值；
（2）写出不等式kx+b＞
的解集．
【答案】（1）k=1，b=﹣1；（2）x＞2或﹣1＜x＜0．
【解析】试题分析：
（1）把A、B两点的坐标代入y=kx+b中列出方程组，即可解得k、b的值；
（2）由一次函数和反比例函数的解析式组合成方程组，解方程组即可求得点C、D的坐标，这样结合图象即可得到所求不等式的解集了.
试题解析：
（1）∵直线y=kx+b过点（1，0）和（0，﹣1），
∴
，
∴k=1，b=﹣1，
（2）由 
解得： 
， 
，
∴C（2，1），D（﹣1，﹣2），
∴不等式
的解集是：x＞2或﹣1＜x＜0．
练习册系列答案
智能训练练测考系列答案
相关题目
【题目】阳光集团新进了20台电视机和30台电饭煲，计划将这50台电器调配给下属的甲、乙两个商店销售，其中40台给甲商店，10台给乙商店.两个商店销售这两种电器每台的利润(元)如下表：
电视机 | 电饭煲 | |
甲商店/元 | 100 | 60 |
乙商店/元 | 80 | 50 |
(1)设集团调配给甲商店x台电视机，则调配给甲商店电饭煲 台，调配给乙商店电视机 台、电饭煲 台；
(2)求出x的取值范围；
(3)如果阳光集团卖出这50台电器想要获得的总利润为3650元，请求出x的值．
