题目内容
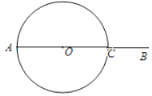
【题目】如图,射线![]() 上有一点
上有一点![]() ,
,![]() ,
,![]() ,点
,点![]() 从点
从点![]() 出发以每秒3个单位长度的速度沿射线
出发以每秒3个单位长度的速度沿射线![]() 运动,过点
运动,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,在射线
,在射线![]() 上取点
上取点![]() ,使得
,使得![]() ,连结
,连结![]() .设点
.设点![]() 的运动时间是
的运动时间是![]() (秒)(
(秒)(![]() ).
).
(1)当点![]() 在点
在点![]() 右侧时,求
右侧时,求![]() 、
、![]() 的长. (用含
的长. (用含![]() 的代数式表示)
的代数式表示)
(2)连结![]() ,设
,设![]() 的面积为
的面积为![]() 平方单位,求
平方单位,求![]() 与
与![]() 之间的丽数关系式.
之间的丽数关系式.
(3)当![]() 是轴对称图形时,直接写出
是轴对称图形时,直接写出![]() 的值.
的值.
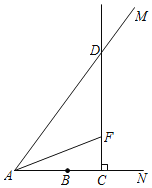
【答案】(1)AD=![]() ,DF= t+5;(2)当0<t<
,DF= t+5;(2)当0<t<![]() 时,S=
时,S=![]() ;当t>
;当t>![]() 时,S=
时,S=![]() ;(3)
;(3)![]() 或
或![]() 或
或![]() .
.
【解析】
(1)解直角三角形求出AD,DC,DF即可.
(2)分两种情形:当0<t<![]() 时,当t>
时,当t>![]() 时,分别求解即可解决问题.
时,分别求解即可解决问题.
(3)分三种情形分别画出图形,构建方程即可解决问题.
(1)在Rt△ACD中,AC=3t,tan∠MAN=![]() ,
,
∴CD=4t.
∴AD=![]() =
=![]() =5t,
=5t,
当点C在点B右侧时,CB=3t5,
∴CF=CB.
∴DF=4t(3t5)=t+5.
(2)当0<t<![]() 时,S=
时,S=![]() (53t)4t=6t2+10t.
(53t)4t=6t2+10t.
当t>![]() 时,S=
时,S=![]() (3t5)4t=6t210t.
(3t5)4t=6t210t.
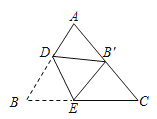
(3)①如图1中,当DF=AD时,△ADF是轴对称图形.
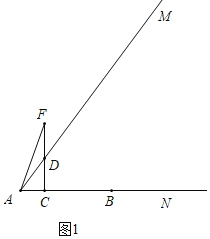
则有53t4t=5t,解得t=![]() ,
,
②如图2中,当AF=DF时,△ADF是轴对称图形.

作FH⊥AD.
∵FA=DF,
∴AH=DH=![]() t,
t,
由cos∠FDH=![]() ,可得
,可得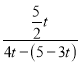 =
=![]() ,解得t=
,解得t=![]() .
.
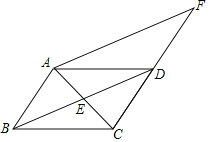
③如图3中,当AF=DF时,△ADF是轴对称图形.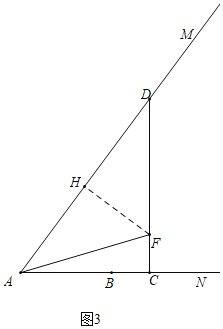
作FH⊥AD.
∵FA=DF,
∴AH=DH=![]() t,
t,
由cos∠FDH=![]() ,可得
,可得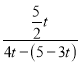 =
=![]() ,解得t=
,解得t=![]() .
.
综上所述,满足条件的t的值为![]() 或
或![]() 或
或![]() .
.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目