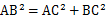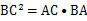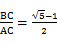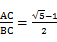题目内容
如图,在直角梯形OABC中,OA∥BC,A、B两点的坐标分别为A(13,0),B(11,12),动点P,Q分别从O、B两点同时出发,点P以每秒2个单位的速度沿OA向终点A运动,点Q以每秒1个单位的速度沿BC向C运动,当点P停止运动时,点Q同时停止运动.线段OB、PQ相交于点D,过点D作DE∥OA,交AB于点E,设动点P、Q运动时间为t(单位:s)
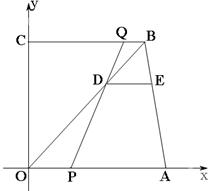
(1)当t为何值时,四边形PABQ是平行四边形,请写出推理过程;
(2)通过推理论证:在P、Q的运动过程中,线段DE的长度不变;

(1)当t为何值时,四边形PABQ是平行四边形,请写出推理过程;
(2)通过推理论证:在P、Q的运动过程中,线段DE的长度不变;
(1)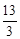 ;(2)推理论证见解析.
;(2)推理论证见解析.
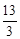 ;(2)推理论证见解析.
;(2)推理论证见解析.试题分析:(1)由PA∥BQ,知当AP=BQ时,四边形PABQ是平行四边形,所以根据AP=BQ列式求解即可;
(2)根据△BQD∽△OPD和△BDE∽△BOA列比例式即可证明.
试题解析:(1)∵PA∥BQ,∴当AP=BQ时,四边形PABQ是平行四边形.
根据题意,得13-2t=t,解得t=
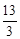 .
.∴当t=
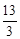 时,四边形PABQ是平行四边形.
时,四边形PABQ是平行四边形.(2)∵OA∥BC,∴△BQD∽△OPD.∴
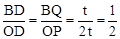 .∴
.∴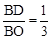 .
.又∵DE∥OA,∴△BDE∽△BOA. ∴
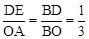 .
.又∵OA="13," ∴
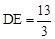 (定值).
(定值).∴在P、Q的运动过程中,线段DE的长度不变.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
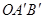 与△OAB是以O为位似中心的位似图形,且位似比为1︰3.
与△OAB是以O为位似中心的位似图形,且位似比为1︰3.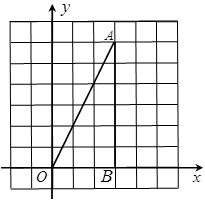
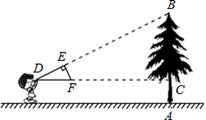

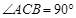 ,
,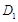 是斜边AB的中点,过
是斜边AB的中点,过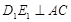 于
于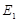 ,连结
,连结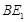 交
交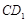 于
于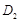 ;过
;过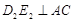 于
于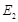 ,连结
,连结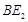 交
交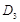 ;过
;过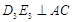 于
于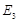 ,…,如此继续,可以依次得到点
,…,如此继续,可以依次得到点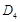 ,
,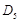 …,
…,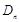 ,分别记
,分别记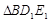 ,
,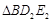 ,
,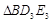 ,…,
,…,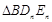 的面积为
的面积为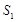 ,
,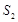 ,
,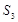 ,…
,…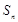 ,则
,则 .
.
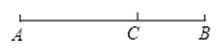
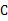 是线段
是线段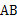 的黄金分割点
的黄金分割点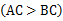 ,则下列结论中正确的是( )
,则下列结论中正确的是( )