��Ŀ����
����Ŀ����֪�Ϧ��Ķ�������n���ε����ĵ�O�����Ϧ����Ŷ���O��ת���ǵ���������n�� �ε����߷ֱ��ڵ�M��N���Ϧ�����n�����ص��������ΪS��
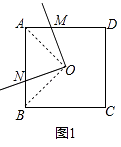
��1����n=4���߳�Ϊ2���Ϧ�=90��ʱ����ͼ��1������ֱ��д��S��ֵ��
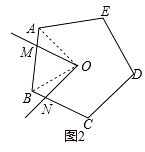
��2����n=5���Ϧ�=72��ʱ����ͼ��2������������ת�����У�S�Ƿ����仯����˵�����ɣ�
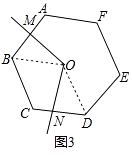
��3����n=6���Ϧ�=120��ʱ����ͼ��3���������S��ԭ������������ļ���֮��������˵�����ɣ������Ϧ���ƽ������BC�߽��ڵ�P���ж��ı���OMPN����״����˵�����ɣ�
���𰸡�
��1��
�⣺��ͼ1������OA��OB��
��n=4ʱ���ı���ABCD�������Σ�
��OA=OB��AO��BO��
���AOB=90�㣬
���AON+��BON=90�㣬
�ߡ�MON=�Ϧ�=90�㣬
���AON+��AOM=90�㣬
���BON=��AOM��
��O��������ABCD�����ģ�
���OAM=��ABO=45�㣬
�ڡ�AOM�͡�BON�У�
�� 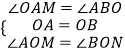 ��
��
���AOM�ա�BON��ASA����
��S��AOM=S��BON��
��S��AOM+S��AON=S��BON+S��AON��
��S�ı���ANDM=S��ABO=S��
��������ABCD�ı߳�Ϊ2��
��S������ABCD=2��2=4��
��S=S��ABO= ![]() S������ABCD=
S������ABCD= ![]() ��4=1
��4=1
��2��
�⣺��ͼ2������ת�����У��Ϧ�����n�����ص����ֵ����S���䣬
�������£�����OA��OB��
��OA=OB=OC����AOB=��MON=72�㣬
���AOM=��BON���ҡ�OAB=��OBC=54�㣬
���OAM�ա�OBN��
���ı���OMBN�������S=S��OBN+S��OBM=S��OAM+S��OBM=S��OAB��
��S�Ĵ�С����
��3��
�⣺���룺S��ԭ������������� ![]() �������ǣ�
�������ǣ�
��ͼ3������OB��OD��
ͬ���á�BOM�ա�DON��
��S=S��BOM+S�ı���OBCN=S��DON+S�ı���OBCN=S�ı���OBCD= ![]() S������ABCDEF��
S������ABCDEF��
�ı���OMPN�����Σ�
�������£�
��ͼ4�����Ϧ���ƽ������BC�߽��ڵ�P��
����OA��OB��OC��OD��PM��PN��
��OA=OB=OC=OD����AOB=��BOC=��COD=��MOP=��PON=60�㣬
���OAM=��OBP=��OCN=60�㣬��AOM=��BOP=��CON��
���OAM�ա�OBP�ա�OCN��
��OM=OP=ON��
���OMP�͡�OPN���ǵȱ������Σ�
��OM=PM=OP=ON=PN��
���ı���OMPN�����Σ�

����������1����ͼ1�����ӶԽ���OA��OB��֤����AOM�ա�BON��ASA������S��AOM=S��BON �� ����S=S��ABO= ![]() S������ABCD=
S������ABCD= ![]() ��4=1����2����ͼ2������ת�����У��Ϧ�����n�����ص����ֵ����S���䣬����OA��OB��ͬ��֤����OAM�ա�OBN����S=S��OBN+S��OBM=S��OAM+S��OBM=S��OAB �� ��S�Ĵ�С���䣻��3����ͼ3��120���൱���������Ľǣ���������Ϊһ�����Ľ�������ת���Σ���ǰ���ʵ������ã���תһ�����Ľ�ʱ�ص����ֵ������ԭ����n���������
��4=1����2����ͼ2������ת�����У��Ϧ�����n�����ص����ֵ����S���䣬����OA��OB��ͬ��֤����OAM�ա�OBN����S=S��OBN+S��OBM=S��OAM+S��OBM=S��OAB �� ��S�Ĵ�С���䣻��3����ͼ3��120���൱���������Ľǣ���������Ϊһ�����Ľ�������ת���Σ���ǰ���ʵ������ã���תһ�����Ľ�ʱ�ص����ֵ������ԭ����n��������� ![]() ����S��ԭ�������������
����S��ԭ������������� ![]() ��Ҳ������ȣ�1����2��֤����OAM�ա�OBN�����ø��������ۣ�
��Ҳ������ȣ�1����2��֤����OAM�ա�OBN�����ø��������ۣ�
�ı���OMPN�����Σ�
�������£���ͼ4�����Ϧ���ƽ������BC�߽��ڵ�P���������߹���ȫ�������Σ�ͬ��֤����OAM�ա�OBP�ա�OCN���á�OMP�͡�OPN���ǵȱ������Σ���OM=PM=OP=ON=PN�������ı���ȵ��ı������οɵã��ı���OMPN�����Σ�
�����㾫����������Ĺؼ�����������ת�����ʵ����֪ʶ�����բ���ת���Ӧ���߶γ��̲��䣬��ת�Ƕȴ�С���䣻����ת���Ӧ�ĵ㵽��ת����ת���ĵľ��벻�䣻����ת�������ͼ�β��䣬ֻ��λ�ñ��ˣ�





