��Ŀ����
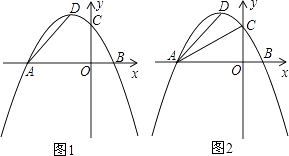
����Ŀ����ͼ1����OΪֱ��AB��һ�㣬����O������OC��ʹ��BOC��120�㣬��һֱ�����ǰ��ֱ�Ƕ�����ڵ�O����һ��OM������OB�ϣ���һ��ON��ֱ��AB���·���
��1����ͼ1�е����ǰ��Ƶ�O��ʱ����ת��ͼ2��ʹһ��OM�ڡ�BOC���ڲ�����ǡ��ƽ�֡�BOC����ON�ķ����ӳ���ΪOD�����COD���� ���㣬��AOD���� ���㣮
��2����ͼ1�е����ǰ��Ƶ�O˳ʱ����ת��ͼ3��ʹON�ڡ�AOC���ڲ������AOM����NOC�Ķ�����

���𰸡���1��30��30��2��30��
��������
��1�����ݽ�ƽ���ߵĶ�������COD����AOD�Ķ�����
��2�����������֪��AOM-��NOC=����AOM+��AON��-����NOC+��AON�������˼��㼴����⣮
��1���ߡ�BOC��120�㣬
���AOC��180�㩁120�㣽60�㣬
��OMǡ��ƽ�֡�BOC��
���COD��30�㣬��AOD��30�㣮
��2����AOM����NOC
������AOM+��AON��������NOC+��AON��
��90�㩁60��
��30�㣮

��ϰ��ϵ�д�
 ��ǰ�κ�ͬ����ϰϵ�д�
��ǰ�κ�ͬ����ϰϵ�д� ����С��ҵϵ�д�
����С��ҵϵ�д� �Ƹ�С״Ԫ����������ϰ��ϵ�д�
�Ƹ�С״Ԫ����������ϰ��ϵ�д� �ɹ�ѵ���ƻ�ϵ�д�
�ɹ�ѵ���ƻ�ϵ�д� ����ѵ����ֱͨ�п�����ϵ�д�
����ѵ����ֱͨ�п�����ϵ�д�
�����Ŀ