题目内容
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 内,
内,![]() ,
,![]() ,点
,点![]() 在
在![]() 外,
外,![]() ,
,![]() .
.
(1)求![]() 的度数;
的度数;
(2)判断![]() 的形状并加以证明;
的形状并加以证明;
(3)连接![]() ,若
,若![]() ,
,![]() ,求
,求![]() 的长.
的长.

【答案】(1) 150°;(2) △ABE是等边三角形,理由见解析;(3)4
【解析】
(1)首先证明△DBC是等边三角形,推出∠BDC=60°,再证明△ADB≌△ADC,推出∠ADB=∠ADC即可解决问题.
(2)结论:△ABE是等边三角形.只要证明△ABD≌△EBC即可.
(3)首先证明△DEC是含有30度角的直角三角形,求出EC的长,理由全等三角形的性质即可解决问题.
(1)解:∵BD=BC,∠DBC=60°,
∴△DBC是等边三角形,∴DB=DC,∠BDC=∠DBC=∠DCB=60°,
在△ADB和△ADC中,
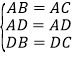 ,
,
∴△ADB≌△ADC,∴∠ADB=∠ADC,∴∠ADB=![]() (360°﹣60°)=150°.
(360°﹣60°)=150°.
(2)解:结论:△ABE是等边三角形.
理由:∵∠ABE=∠DBC=60°,∴∠ABD=∠CBE,
在△ABD和△EBC中,
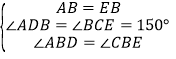 ,
,
∴△ABD≌△EBC,∴AB=BE,∵∠ABE=60°,∴△ABE是等边三角形.
(3)解:连接DE.

∵∠BCE=150°,∠DCB=60°,∴∠DCE=90°,∵∠EDB=90°,∠BDC=60°,
∴∠EDC=30°,∴EC=![]() DE=4,∵△ABD≌△EBC,∴AD=EC=4.
DE=4,∵△ABD≌△EBC,∴AD=EC=4.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目






